题目内容
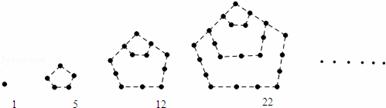
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,若an=145,则n= .
10
解:a2﹣a1=5﹣1=4,a3﹣a2=12﹣5=7,a4﹣a3=22﹣12=10,…,由此可知数列{an+1﹣an}构成以4为首项,以3为公差的等差数列.所以an+1﹣an=4+3(n﹣1)=3n+1.a2﹣a1=3×1+1
a3﹣a2=3×2+1…an﹣an﹣1=3(n﹣1)+1累加得:an﹣a1=3(1+2+…+(n﹣1))+n﹣1
所以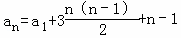 =1+
=1+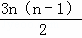 +n﹣1=
+n﹣1=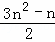 .由
.由 ,解得:
,解得: .故答案为10.
.故答案为10.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
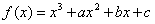 ,在定义域
,在定义域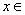 [-2,2]上表
[-2,2]上表 示的曲线过原点,且在x=±1处的切线斜率均为
示的曲线过原点,且在x=±1处的切线斜率均为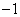 .有以下命题:①
.有以下命题:①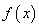 是奇函数;②若
是奇函数;②若 内递减,则
内递减,则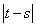 的最大值为4;③
的最大值为4;③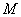 ,最小值为
,最小值为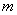 ,则
,则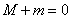 ; ④若对
; ④若对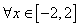 ,
,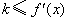 恒成立,则
恒成立,则 的最大值为2.其中正确命题的个数为
的最大值为2.其中正确命题的个数为  的前
的前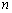 项和为
项和为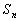 ,若
,若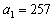 ,且满足
,且满足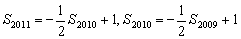 ,则使
,则使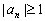 的
的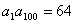

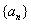 是等比数列,
是等比数列,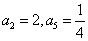 ,则
,则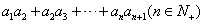 的值范围是_________
的值范围是_________ ______
______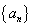 是等差数列,它的前
是等差数列,它的前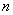 项和
项和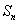 满足:
满足: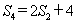 ,令
,令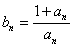 .若对任意的
.若对任意的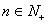 ,都有
,都有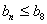 成立,则
成立,则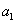 的取值范围是
的取值范围是 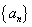 满足
满足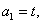 ,
,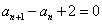
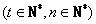 ,记数列
,记数列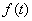 ,则
,则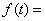 .
.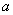 n}满足:
n}满足: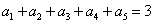 ,
,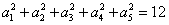 ,则
,则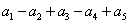 的值是( ) A.
的值是( ) A. 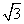 B.
B.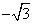 C.
C. 4 D.2
4 D.2  ,都有
,都有 (
( 为常数),那么这个数列叫做等积数列,
为常数),那么这个数列叫做等积数列, 是等积数列,且
是等积数列,且 ,公积为8,则
,公积为8,则 .
.