题目内容
5.已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{{\sqrt{2}}}{2}$,同时椭圆C上存在一点与右焦点关于直线x+y-1=0对称,则椭圆C的方程为( )| A. | $\frac{{8{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$ | B. | $\frac{{9{x^2}}}{8}+\frac{{16{y^2}}}{9}=1$ | C. | $\frac{{8{x^2}}}{9}+\frac{{9{y^2}}}{16}=1$ | D. | $\frac{{9{x^2}}}{8}+\frac{{9{y^2}}}{16}=1$ |
分析 由椭圆的离心率,求得b=c,则椭圆的标准方程转化成x2+2y2=2b2,求得右焦点关于直线x+y-1=0对称的点,代入椭圆方程,即可求得b和a的值,求得椭圆方程.
解答 解:由椭圆的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,则a=$\sqrt{2}$c,
由b2=a2-c2=c2,则b=c,
则设椭圆方程为x2+2y2=2b2,
∴右焦点(b,0)关于l:y=-x+1的对称点设为(x′,y′),则$\left\{\begin{array}{l}{\frac{y′}{x′-b}=1}\\{\frac{y′}{2}=-\frac{x′+b}{2}+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x′=1}\\{y′=1-b}\end{array}\right.$,
由点(1,1-b)在椭圆上,得1+2(1-b)2=2b2,b2=$\frac{9}{16}$,a2=$\frac{9}{8}$,
∴椭圆的标准方程为:$\frac{8{x}^{2}}{9}+\frac{{16y}^{2}}{9}=1$,
故选:A.
点评 本题考查椭圆的标准方程及简单几何性质,考查点关于直线对称的求法,考查计算能力,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
13.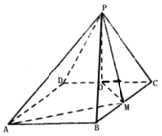 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.函数f(x)=$\frac{{sinx\sqrt{1-|x|}}}{{|{x+2}|-2}}$的奇偶性是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |