题目内容
已知连续不断函数f(x)=cosx-x,x∈(0,
),g(x)=sinx+x-
,x∈(0,
),h(x)=xsinx+x-
,x∈(0,
)
(1)证明:函数f(x)在区间(0,
)上有且只有一个零点;
(2)现已知函数g(x),h(x)在(0,
)上单调递增,且都只有一个零点(不必证明),记三个函数f(x),g(x),h(x)的零点分别为x1,x2,x3.
求证:①x1+x2=
;
②判断x2与x3的大小,并证明你的结论.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(1)证明:函数f(x)在区间(0,
| π |
| 2 |
(2)现已知函数g(x),h(x)在(0,
| π |
| 2 |
求证:①x1+x2=
| π |
| 2 |
②判断x2与x3的大小,并证明你的结论.
考点:函数零点的判定定理,函数单调性的性质
专题:函数的性质及应用
分析:(1)由零点存在性定理知f(x)在区间(0,
)上有零点,运用单调性定义证明;f(x)在(0,
)上是单调递减函数.
(2)将其变形为:cos(
-x2)-(
-x2)=0,即f(
-x2)=0,在(0,
)上有唯一零点,从而有
-x2=x1,x1+x2=
,
Ⅰ)因为x2是g(x)的零点,所以有sinx2+x2-
=0,
Ⅱ)判断x2<x3,运用零点存在性定理和定义判断证明即可.
| π |
| 2 |
| π |
| 2 |
(2)将其变形为:cos(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
Ⅰ)因为x2是g(x)的零点,所以有sinx2+x2-
| π |
| 2 |
Ⅱ)判断x2<x3,运用零点存在性定理和定义判断证明即可.
解答:
解:(1)先证明f(x)在区间(0,
)上有零点:由于f(0)=1>0,f(
)=-
,
由零点存在性定理知f(x)在区间(0,
)上有零点,
再证明f(x)在(0,
)上是单调递减函数:
设0<x1<x2<
,
f(x1)-f(x2)=(cosxx-x1)-(cosx2-x2)=(cosx1-cosx2)-(x1-x2)
由于y=cosx在(0,
)上递减,
所以cosx1-cosx2>0又-(x1-x2)>0
从而f(x1)>f(x2),
即f(x)在(0,
)上是单调递减函数.
故函数f(x)在(0,
)有且只有一个零点,
(2)Ⅰ)因为x2是g(x)的零点,所以有sinx2+x2-
=0,
将其变形为:cos(
-x2)-(
-x2)=0,即f(
-x2)=0,
从而有f(
-x2)=f(x1)=0,
又因为
-x2,x1∈(0,
),且由(1)的结论f(x)
在(0,
)上有唯一零点,
从而有
-x2=x1,x1+x2=
,
Ⅱ)判断x2<x3,证明如下:由于h(0)=-
<0,h(1)=sin1=1-
>sin
+1-
=
+1-
,
由零点存在性定理和已知得0<x3<1,
从而有 0=x3sinx3+x3-
<sinx3+x3-
=g(x3),g(x2)=0
所以有g(x2)<g(x3),
又由已知g(x)在(0,
)上单调递增,所以x2<x3.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
由零点存在性定理知f(x)在区间(0,
| π |
| 2 |
再证明f(x)在(0,
| π |
| 2 |
设0<x1<x2<
| π |
| 2 |
f(x1)-f(x2)=(cosxx-x1)-(cosx2-x2)=(cosx1-cosx2)-(x1-x2)
由于y=cosx在(0,
| π |
| 2 |
所以cosx1-cosx2>0又-(x1-x2)>0
从而f(x1)>f(x2),
即f(x)在(0,
| π |
| 2 |
故函数f(x)在(0,
| π |
| 2 |
(2)Ⅰ)因为x2是g(x)的零点,所以有sinx2+x2-
| π |
| 2 |
将其变形为:cos(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
从而有f(
| π |
| 2 |
又因为
| π |
| 2 |
| π |
| 2 |
在(0,
| π |
| 2 |
从而有
| π |
| 2 |
| π |
| 2 |
Ⅱ)判断x2<x3,证明如下:由于h(0)=-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
由零点存在性定理和已知得0<x3<1,
从而有 0=x3sinx3+x3-
| π |
| 2 |
| π |
| 2 |
所以有g(x2)<g(x3),
又由已知g(x)在(0,
| π |
| 2 |
点评:本题综合考查了函数的性质,零点问题,分类转化,不等式问题,综合性较强,难度较大,属于难题.

练习册系列答案
相关题目
已知数列{an}的通项公式是an=
(n∈N*),若an+an+1=
-3,则n的值是( )
| 1 | ||||
|
| 11 |
| A、10 | B、9 | C、8 | D、6 |
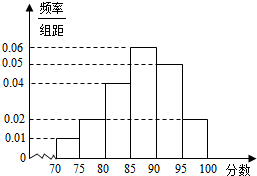 某校为规范学生的行为,制定出一套科学有效的“德语百分制量化考核制度”,一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200,现将编号能被30整除的40名学生抽取出来进行座谈,并将他们的考核分分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],统计后得到如图的频率分布直方图:
某校为规范学生的行为,制定出一套科学有效的“德语百分制量化考核制度”,一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200,现将编号能被30整除的40名学生抽取出来进行座谈,并将他们的考核分分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],统计后得到如图的频率分布直方图: