题目内容
19.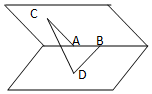 如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 由$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,两边平方后展开整理,即可求得${\overrightarrow{CD}}^{2}$,则CD的长可求.
解答 解:∵$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}={\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}$+2$\overrightarrow{CA}•\overrightarrow{AB}$+2$\overrightarrow{CA}•\overrightarrow{BD}$+2$\overrightarrow{AB}•\overrightarrow{BD}$,
∵$\overrightarrow{CA}$⊥$\overrightarrow{AB}$,$\overrightarrow{BD}$⊥$\overrightarrow{AB}$,
∴$\overrightarrow{CA}•\overrightarrow{AB}=0$,$\overrightarrow{BD}•\overrightarrow{AB}=0$,
$\overrightarrow{CA}•\overrightarrow{BD}=|\overrightarrow{CA}||\overrightarrow{BD}|$cos120°=-$\frac{1}{2}$×1×2=-1.
∴${\overrightarrow{CD}}^{2}=1+1+4$-2×1=4,
∴|$\overrightarrow{CD}$|=2,
故选:A.
点评 本题考查了向量的多边形法则、数量积的运算性质、向量垂直与数量积的关系,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案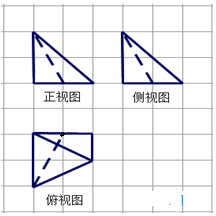 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 不能确定 |
| A. | 2n-1-2 | B. | 2n-2 | C. | 2n-1-2n | D. | -2n-1 |
| A. | y=|sinx| | B. | $y=cos({2x+\frac{π}{2}})$ | C. | y=sin2x+cos2x | D. | y=sinx-cosx |
| A. | 25 | B. | 49 | C. | 15 | D. | 40 |
