题目内容
7.给出命题p:方程$\frac{x^2}{a}+\frac{y^2}{2-a}=1$表示焦点在y轴上的椭圆;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.(1)如果命题p为真,求a的取值范围;
(2)如果命题“p∪q”为真,“p∩q”为假,求实数a的取值范围.
分析 (1)若命题p为真,则2-a>a>0,解得:a的取值范围;
(2)如果命题“p∪q”为真,“p∩q”为假,则p,q中一真一假,进而可得实数a的取值范围.
解答 解:(1)命题p为真?2-a>a>0?0<a<1…(4分)
(2)命题q为真$?△={(2a-3)^2}-4>0?a<\frac{1}{2}或a>\frac{5}{2}$
命题“p∨q”为真,“p∧q”为假?p,q中一真一假,…(6分)
当p真q假时,$\left\{{\begin{array}{l}{0<a<1}\\{\frac{1}{2}≤a≤\frac{5}{2}}\end{array}}\right.$,得$\frac{1}{2}≤a<1$…(8分)
当p假q真时,$\left\{{\begin{array}{l}{a≤0或a≥1}\\{a<\frac{1}{2}或a>\frac{5}{2}}\end{array}}\right.$,得$a≤0或a>\frac{5}{2}$
所以a的取值范围是$\frac{1}{2}≤a<1$或$a≤0或a>\frac{5}{2}$…(10分)
点评 本题以命题的真假判断与应用为载体,考查了椭圆的标准方程,二次函数的图象和性质,难度中档.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.f(x)=Asin(ωx+ωπ)(A>0,ω>0)在$[{-\frac{3π}{2},-\frac{3π}{4}}]$上单调,则ω的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{4}{3}$ |
12.已知f(x)=tan(2x+$\frac{π}{4}$),则使f(x)≥$\sqrt{3}$成立的x的集合是( )
| A. | [$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z | B. | (-$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{π}{24}$+$\frac{1}{2}$kπ),k∈Z | ||
| C. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ),k∈Z | D. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ],k∈Z |
19.如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( ) 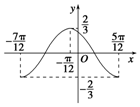

| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
17.为了得到函数y=sin2x+cos2x的图象,可以将函数y=cos2x-sin2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
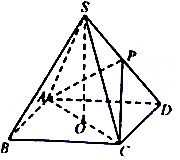 如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.
如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.