题目内容
16.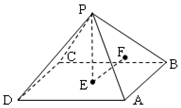 如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.
如图,P-ABCD是棱长均为1的正四棱锥,顶点P在平面ABCD内的正投影为点E,点E在平面PAB内的正投影为点F,则 tan∠PEF=$\sqrt{2}$.
分析 取AB中点G,连接EG,可证得平面PAB⊥平面PEG,过E作EF⊥PG,垂足为F,则EF⊥平面ABP,即F为E在平面PAB上的投影,然后求解直角三角形得答案.
解答 解:如图,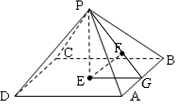
取AB中点G,连接EG,则EG⊥AB,又PE⊥平面ABCD,∴PE⊥AB,
∵PE∩EG=E,∴AB⊥平面PEG,则平面PAB⊥平面PEG,且平面PEG∩平面PAB于PG.
过E作EF⊥PG,垂足为F,则EF⊥平面ABP,即F为E在平面PAB上的投影.
在Rt△PEG与Rt△PFE中,可得∠PEF=∠PGE.
∵P-ABCD是棱长均为1的正四棱锥,∴EG=$\frac{1}{2}$,PE=$\frac{\sqrt{2}}{2}$.
∴tan∠PEF=$\frac{PE}{EG}=\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}=\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查线面角的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.抛物线E:y2=2px(p>0)的焦点为F,点A(0,2),若线段AF的中点B在抛物线上,则|BF|=( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{2}}{4}$ |
1.若直线AB的方程为$\sqrt{3}$x+y-7=0,则直线AB的倾斜角是( )
| A. | 135° | B. | 120° | C. | 60° | D. | 45° |
8.已知集合$A=\{x|\frac{x+3}{x-3}≤0\}$,B={x|x-1≥0},则A∩B为( )
| A. | [1,3] | B. | [1,3) | C. | [-3,∞) | D. | (-3,3] |
