题目内容
设关于x的一元二次方程ax2-2bx+a=0(a,b∈R)
(Ⅰ)若a是集合{1,2,3}中任取一个元素,b是从集合{1,2,3}中任取一个元素,求上述方程有两个不相等实数根的概率.
(Ⅱ)若a是从区间(0,3)任取的一个实数,b是从区间(0,2)任取的一个实数,求上述方程没有实数根的概率.
(Ⅰ)若a是集合{1,2,3}中任取一个元素,b是从集合{1,2,3}中任取一个元素,求上述方程有两个不相等实数根的概率.
(Ⅱ)若a是从区间(0,3)任取的一个实数,b是从区间(0,2)任取的一个实数,求上述方程没有实数根的概率.
考点:几何概型,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(Ⅰ)为古典概型,只需列举出所有的基本事件和符合条件的基本事件,作比值即可;
(Ⅱ)为几何概型,作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
(Ⅱ)为几何概型,作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
解答:
解:(Ⅰ)∵a为取集合{1,2,3}中任一个元素,b为取集合{1,2,3}中任一个元素,
∴a,b的取值的情况有(1,1),(1,2),(1,3),(2,1),(2,2)(2,3),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值,即基本事件总数为:9.
设“方程f(x)=0有两个不相等的实根”为事件A,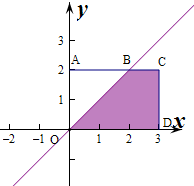
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为:a>2b.
当a>2b时,a,b取值的情况有(3,1),即A包含的基本事件数为:1,
∴方程有两个不相等实数根的概率
.
(Ⅱ)若a从区间(0,3)中任取一个数,b从区间(0,2)中任取一个数,
则0<a<3且0<b<2,对应的区域为矩形,面积S=3×2=6,
方程f(x)=0没有实根,则△=4b2-4a2<0,即b2<a2,∴b<a,
作出不等式组对应的平面区域如图:
则B(2,2),C(3,2),D(3,0),
则题型BCDO的面积S=
×2=4
则由几何概型的概率公式可得方程f(x)=0没有实根
.
∴a,b的取值的情况有(1,1),(1,2),(1,3),(2,1),(2,2)(2,3),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值,即基本事件总数为:9.
设“方程f(x)=0有两个不相等的实根”为事件A,
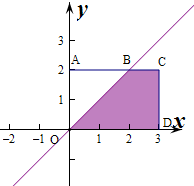
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为:a>2b.
当a>2b时,a,b取值的情况有(3,1),即A包含的基本事件数为:1,
∴方程有两个不相等实数根的概率
| 1 |
| 9 |
(Ⅱ)若a从区间(0,3)中任取一个数,b从区间(0,2)中任取一个数,
则0<a<3且0<b<2,对应的区域为矩形,面积S=3×2=6,
方程f(x)=0没有实根,则△=4b2-4a2<0,即b2<a2,∴b<a,
作出不等式组对应的平面区域如图:
则B(2,2),C(3,2),D(3,0),
则题型BCDO的面积S=
| 1+3 |
| 2 |
则由几何概型的概率公式可得方程f(x)=0没有实根
| 2 |
| 3 |
点评:本题主要考查概率的计算,根据古典关系和几何概型的概率公式是解决本题的关键.

练习册系列答案
相关题目
计算2sin15°•cos30°+sin15°等于( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
由①y=2x+5是一次函数;②y=2x+5的图象是一条直线;③一次函数的图象是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是( )
| A、②①③ | B、③①② |
| C、①②③ | D、②③① |
 选修4.1:几何证明选讲
选修4.1:几何证明选讲