题目内容
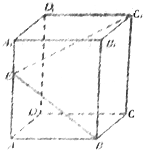长方体ABCD-A1B1C1D1的底面是边长为a的正方形，若在侧棱AA1上至少存在一点E，使得∠C1EB=90°，则侧棱AA1的长的最小值为（ ）| A、a | B、2a | C、3a | D、4a |
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：设侧棱AA1的长为x，A1E=t，则AE=x-t，由已知得t2-xt+a2=0，由此利用根的判别式能求出侧棱AA1的长的最小值．
解答：
解：设侧棱AA1的长为x，A1E=t，则AE=x-t，
∵长方体ABCD-A1B1C1D1的底面是边长为a的正方形，
∠C1EB=90°，
∴C1E2+BE2=BC12，
∴2a2+t2+a2+（x-t）2=a2+x2，
整理，得：t2-xt+a2=0，
∵在侧棱AA1上至少存在一点E，使得∠C1EB=90°，
∴△=（-x）2-4a2≥0，
解得x≥2a．
∴侧棱AA1的长的最小值为2a．
故选：B．
∵
长方体ABCD-A1B1C1D1的底面是边长为a的正方形，∠C1EB=90°，
∴C1E2+BE2=BC12，
∴2a2+t2+a2+（x-t）2=a2+x2，
整理，得：t2-xt+a2=0，
∵在侧棱AA1上至少存在一点E，使得∠C1EB=90°，
∴△=（-x）2-4a2≥0，
解得x≥2a．
∴侧棱AA1的长的最小值为2a．
故选：B．
点评：本题考查长方体的侧棱长的最小值的求法，是中档题，解题时要注意根的判别式的合理运用．
练习册系列答案
相关题目
如图，在△ABC中，线段BE，CF交于点P，设向量| AB |
| a |
| AC |
| b |
| AP |
| c |
| AF |
| 2 |
| 3 |
| a |
| AE |
| 1 |
| 2 |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
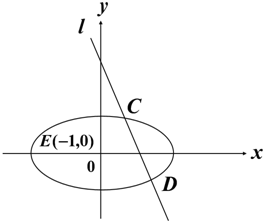已知椭圆