题目内容
7.设F为抛物线y2=8x的焦点,A、B、C为该抛物线上不同的三点,且$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,O为坐标原点,若△OFA、△OFB、△OFC的面积分别为S1、S2、S3,则S12+S22+S32=( )| A. | 36 | B. | 48 | C. | 54 | D. | 64 |
分析 确定抛物线y2=8x的焦点F的坐标,求出S12+S22+S32的表达式,利用点F是△ABC的重心,求得数值.
解答  解:设A、B、C三点的坐标
解:设A、B、C三点的坐标
分别为(x1,y1),(x2,y2),(x3,y3),
∵抛物线y2=8x的焦点F的坐标为(2,0),
∴S1=$\frac{1}{2}$×|y1|×2=|y1|,
S2=$\frac{1}{2}$×|y2|×2=|y2|,
S3=$\frac{1}{2}$×|y3|×2=|y3|,
∴S12+S22+S32=y12+y22+y32=8(x1+x2+x3);
∵$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$,
∴点F是△ABC的重心,
∴$\frac{1}{3}$(x1+x2+x3)=p=2,
∴(x1+x2+x3)=6;
∴S12+S22+S32=6×8=48.
故选:B.
点评 本题考查抛物线的定义与性质的应用问题,也考查了三角形重心的性质,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知数列{an}各项的绝对值均为1,Sn为其前n项和.若S7=3,则该数列{an}的前七项的可能性有( )种.
| A. | 10 | B. | 20 | C. | 21 | D. | 42 |
15.已知点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
| A. | -7<a<24 | B. | -24<a<7 | C. | a<-1或a>24 | D. | a<-24或a>7 |
2.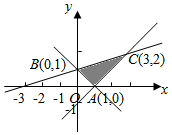 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
12.设(1+x)n=a0+a1x+a2x2+…+anxn,若a1+a2+…+an=63,则展开式中系数最大项是( )
| A. | 20 | B. | 20x3 | C. | 105 | D. | 105x4 |
8.设an=-n2+9n+10,则数列{an}前n项和最大时n的值为( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 12 |
 如图,在四棱锥P-ABCD中,侧棱长均相等且为$\sqrt{2}$,DA=DC=$\sqrt{3}$,AB=BC=1.
如图,在四棱锥P-ABCD中,侧棱长均相等且为$\sqrt{2}$,DA=DC=$\sqrt{3}$,AB=BC=1.