题目内容
有下列四个命题:
①设A、B为两个定点,k为正常数,|
|+|
|=k,则动点P的轨迹为椭圆;
②抛物线y=-
x2的焦点坐标是(-
,0);
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为抛物线.
其中正确命题为( )
①设A、B为两个定点,k为正常数,|
| PA |
| PB |
②抛物线y=-
| 1 |
| 2 |
| 1 |
| 8 |
③“若q≤1,则x2+2x+q=0有实根”的逆否命题;
④若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为抛物线.
其中正确命题为( )
| A、①③ | B、②④ | C、③④ | D、①② |
考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程
分析:①根据椭圆的定义,当k>|AB|时是椭圆;②抛物线y=-
的化标准方程求焦点坐标,③写出逆否命题判断,④由点P到直线x=-1的距离比它到点(2,0)的距离小1知点P到直线x=-2的距离比它到点(2,0)的距离相等,符合抛物线定义.
| 1 |
| 2 |
解答:
解;①根据椭圆的定义,当K≤|AB|时,动点P的轨迹不是椭圆,∴①错误;
②抛物线y=-
的化为标准方程x2=2y,焦点坐标是(0,
),②错误;
③“若q≤1,则x2+2x+q=0有实根”的逆否命题是“若x2+2x+q=0无实根,则q>1”,x2+2x+q=0无实根?△<0,解得q>1,为真命题,③正确;
④由点P到直线x=-1的距离比它到点(2,0)的距离小1知点P到直线x=-2的距离比它到点(2,0)的距离相等,即P的轨迹为以(2,0)为焦点,X=-2为准线的抛物线.④正确;
故选;C.
②抛物线y=-
| 1 |
| 2 |
| 1 |
| 2 |
③“若q≤1,则x2+2x+q=0有实根”的逆否命题是“若x2+2x+q=0无实根,则q>1”,x2+2x+q=0无实根?△<0,解得q>1,为真命题,③正确;
④由点P到直线x=-1的距离比它到点(2,0)的距离小1知点P到直线x=-2的距离比它到点(2,0)的距离相等,即P的轨迹为以(2,0)为焦点,X=-2为准线的抛物线.④正确;
故选;C.
点评:本题主要考查了圆锥曲线的中椭圆与抛物线的定义和性质,考查的知识点较多,属于中档题.

练习册系列答案
相关题目
已知幂函数y=f(x)的图象过点(2,8),则f(5)的值为( )
| A、243 | B、125 |
| C、40 | D、25 |
复数1+
在复平面上对应的点的在( )
| 1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数f(x)=x(x2-1)的图象大致是( )
A、 |
B、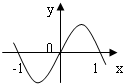 |
C、 |
D、 |
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| C、命题“a、b都是有理数”的否定是“a、b都不是有理数” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |