题目内容
已知点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,则下列说法中正确的是( )
①3a-4b+10>0
②当a>0时,a+b有最小值,无最大值
③
>2
④当a>0且a≠1时,
的取值范围为(-∞,-
)∪(
,+∞)
①3a-4b+10>0
②当a>0时,a+b有最小值,无最大值
③
| a2+b2 |
④当a>0且a≠1时,
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
| A、①③ | B、③④ | C、②④ | D、②③ |
考点:命题的真假判断与应用,直线的斜率
专题:不等式的解法及应用
分析:根据点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,可以画出点A(a,b)所在的平面区域,进而结合二元一次不等式的几何意义,两点之间距离公式的几何意义,及两点之间连线斜率的几何意义,逐一分析四个答案.可得结论.
解答:
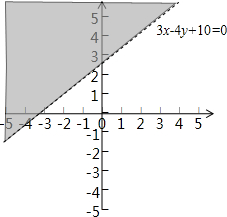 解:∵点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
解:∵点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
故点A(a,b)在如图所示的平面区域内
故3a-4b+10<0,即①错误;
当a>0时,a+b>
,a+b即无最小值,也无最大值,故②错误;
设原点到直线3x-4y+10=0的距离为d,则d=
=2,则
>d=2,故③正确;
当a>0且a≠1,b>0时,
表示点A(a,b)与B(1,0)连线的斜率,
∵当a=0,b=
时,
=-
,又∵直线3x-4y+10=0的斜率为
,
故
的取值范围为(-∞,-
)∪(
,+∞),故④正确;
故答案为:③④.
 解:∵点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
解:∵点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,故点A(a,b)在如图所示的平面区域内
故3a-4b+10<0,即①错误;
当a>0时,a+b>
| 5 |
| 2 |
设原点到直线3x-4y+10=0的距离为d,则d=
| 10 | ||
|
| a2+b2 |
当a>0且a≠1,b>0时,
| b |
| a-1 |
∵当a=0,b=
| 5 |
| 2 |
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
故
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
故答案为:③④.
点评:本题考查了线性规划问题、直线的斜率计算公式及其单调性,考查了问题的转化能力和推理能力,属于中档题.

练习册系列答案
相关题目
已知集合A={0,1,2,3},集合B={x∈N||x|≤2},则A∩B=( )
| A、{3} |
| B、{0,1,2} |
| C、{1,2} |
| D、{0,1,2,3} |
向量
=
或
=
是
•
=0的( )
| a |
| 0 |
| b |
| 0 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要件 |
如果奇函数f(x)在[a,b]具有最大值1,那么该函数在[-b,-a]有( )
| A、最小值1 | B、最小值-1 |
| C、最大值1 | D、最大值-1 |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则f(
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则f(| π |
| 4 |
A、
| ||
| B、0 | ||
| C、1 | ||
D、
|
若等比数列{an}满足a6a8-4a7=0,则a1•a2•a3•…•a13等于( )
| A、213 |
| B、214 |
| C、226 |
| D、228 |
若集合A={y|0≤y<2},B={x||x|>1},则A∩(∁RB)=( )
| A、{x|0≤x≤1} |
| B、{x|1≤x<2} |
| C、{x|-1<x≤0} |
| D、{x|1<x<2} |