题目内容
从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得
xi=80,
yi=20,
xiyi=184,
=720.
1)求家庭的月储蓄y关于月收入x的线性回归方程
=
x+
;
2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
=
,
=
-
.
| 10 |
 |
| i=1 |
| 10 |
 |
| i=1 |
| 10 |
 |
| i=1 |
| 10 |
 |
| i=1 |
| x | 2 i |
1)求家庭的月储蓄y关于月收入x的线性回归方程
| ? |
| y |
| ? |
| b |
| ? |
| a |
2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
考点:线性回归方程
专题:概率与统计
分析:1)利用已知条件求出,样本中心坐标,利用参考公式求出b,a,然后求出线性回归方程:
=bx+a;
2)通过x=7,利用回归直线方程,推测该家庭的月储蓄.
| ? |
| y |
2)通过x=7,利用回归直线方程,推测该家庭的月储蓄.
解答:
(本小题满分12分)
解:1)由题意知n=10,
=
xi=
×80=8,
=
yi=
×20=2
又Ixx=
-n
2=720-10×82=80,Ixy=
xiyi-n
=184-10×8×2=24,
由此得
=
=
=0.3,
=
-
=2-0.3×8=-0.4,
故所求线性回归方程为
=0.3x-0.4.
2)将x=7代入回归方程,可以预测该家庭的月储蓄约为
=0.3×7-0.4=1.7(千元).
解:1)由题意知n=10,
. |
| x |
| 1 |
| n |
| 10 |
 |
| i=1 |
| 1 |
| 10 |
. |
| y |
| 1 |
| n |
| 10 |
 |
| i=1 |
| 1 |
| 10 |
又Ixx=
| 10 |
 |
| i=1 |
| x | 2 i |
. |
| x |
| 10 |
 |
| i=1 |
. |
| x |
. |
| y |
由此得
| ? |
| b |
| Ixy |
| Ixx |
| 24 |
| 80 |
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
故所求线性回归方程为
 |
| y |
2)将x=7代入回归方程,可以预测该家庭的月储蓄约为
 |
| y |
点评:本题考查回归直线方程的求法与应用,基本知识的考查,难度不大.

练习册系列答案
相关题目
已知双曲线的顶点为(2,-1)与(2,5),它的一条渐近线与直线3x-4y=0平行,则双曲线的准线方程是( )
A、y=2±
| ||
B、x=2±
| ||
C、y=2±
| ||
D、x=2±
|
 如图甲所示,点E为矩形ABCD边CD的中点,AB=2,AD=
如图甲所示,点E为矩形ABCD边CD的中点,AB=2,AD=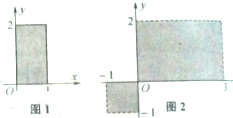 如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合:
如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合: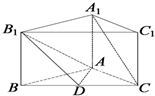 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,