题目内容
已知x1，x2是方程（x-1）2=-1的两相异根，当x1=1-i（i为虚数单位）时，则x22为（ ）
| A、-2i | B、1+i |
| C、2i | D、1-i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由方程（x-1）2=-1化简得到x1+x2=2，然后再由x1的值求出x2，则答案可求．
解答：
解：由（x-1）2=-1，
得x2-2x+2=0．
则x1+x2=2．
∵x1=1-i，
∴1-i+x2=2．
∴x2=1+i．
则x22=(1+i)2=1+2i+i2=2i．
故选：C．
得x2-2x+2=0．
则x1+x2=2．
∵x1=1-i，
∴1-i+x2=2．
∴x2=1+i．
则x22=(1+i)2=1+2i+i2=2i．
故选：C．
点评：本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
函数f（x）的部分图象如图所示，则f（x）的解析式为（ ）
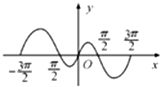
| A、f（x）=x+sinx | ||||
B、f（x）=
| ||||
| C、f（x）=xcosx | ||||
D、f（x）=x（x-
|
已知某个多面体的三视图（单位cm）如图所示，则此多面体的体积是已知全集U=R，A={x|x≤a+2}，B={x|x≥a2}，若∁U（A∩B）=R，则a的取值范围是（ ）
| A、[-1，2] |
| B、（-1，2） |
| C、（-∞，-1]∪[2，+∞） |
| D、（-∞，-1）∪（2，+∞） |
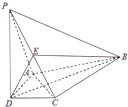如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD⊥DC，DB平分∠ADC，E为PC的中点，AD=CD=1，DB=2
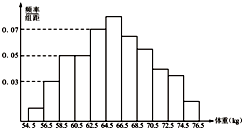为了了解某地区高三学生的身体发育情况，抽查了该地区200名年龄为17.5岁到18岁的男生体重（kg），得到频率分布直方图如图：根据如图可得这200名学生中体重在[56.5，64.5]的学生人数是