题目内容
写出下面数列{an}的前5项:a1=
,an=4an-1+1(n>1).
| 1 |
| 2 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由a1=
,an=4an-1+1(n>1).分别取n=2,3,4,5,即可得出.
| 1 |
| 2 |
解答:
解:由a1=
,an=4an-1+1(n>1).
分别取n=2,3,4,5,
可得a2=4×
+1=3,
a3=4×3+1=13,
a4=13×4+1=53,
a5=53×4+1=213.
| 1 |
| 2 |
分别取n=2,3,4,5,
可得a2=4×
| 1 |
| 2 |
a3=4×3+1=13,
a4=13×4+1=53,
a5=53×4+1=213.
点评:本题考查了递推式的应用,考查了计算能力,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知下列各组命题,其中p是q的充分必要条件的是( )
| A、p:m≤-2或m≥6;q:y=x2+mx+m+3 有两个不同的零点 | ||
B、p:
| ||
| C、p:cosα=cosβ;q:tanα=tanβ | ||
| D、p:A∩B=A; q:A⊆U,B⊆U,∁UB⊆∁UA |
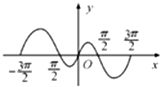
函数f(x)的部分图象如图所示,则f(x)的解析式为( )

| A、f(x)=x+sinx | ||||
B、f(x)=
| ||||
| C、f(x)=xcosx | ||||
D、f(x)=x(x-
|
已知全集U=R,A={x|x≤a+2},B={x|x≥a2},若∁U(A∩B)=R,则a的取值范围是( )
| A、[-1,2] |
| B、(-1,2) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1)∪(2,+∞) |
 已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证:
已知:如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC,垂足为E,连接EA交⊙O于点F.求证: