题目内容
 如图,在直三棱柱ABC-A1B1C1,中,AC=BC=
如图,在直三棱柱ABC-A1B1C1,中,AC=BC=| 1 |
| 2 |
(1)证明:DC1⊥BC;
(2)求二面角C-BC1-D的余弦值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由已知得A1D=AD=2,∠ADC=45°,∠A1DC1=45°,从而DC⊥DC1,又DB⊥DC1,由此能证明DC1⊥BC.
(2)由直三棱柱性质得CC1⊥BC,再由DC1⊥BC,得面DCC1⊥面BCC1,过D作DH⊥CC1于H,过H作HI⊥BC1于I,则∠DIH为所求二面角的平面角,由此能求出二面角C-BC1-D的余弦值.
(2)由直三棱柱性质得CC1⊥BC,再由DC1⊥BC,得面DCC1⊥面BCC1,过D作DH⊥CC1于H,过H作HI⊥BC1于I,则∠DIH为所求二面角的平面角,由此能求出二面角C-BC1-D的余弦值.
解答:
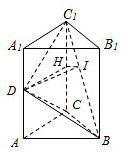 解:(1)证明:∵D是棱AA1的中点,∴A1D=AD=2,
解:(1)证明:∵D是棱AA1的中点,∴A1D=AD=2,
在Rt△DAC中,AC=AD=2,∴∠ADC=45°,
同理,∠A1DC1=45°,∴∠CDC1=90°,∴DC⊥DC1,
又DB⊥DC1,∴DC1⊥面BCD,
∴DC1⊥BC.
(2)解:在直三棱柱ABC-A1B1C1中,CC1⊥BC,
由(1)得DC1⊥BC,∴BC⊥ACC1A1,∴面DCC1⊥面BCC1,
过D作DH⊥CC1于H,过H作HI⊥BC1于I,
则∠DIH为所求二面角的平面角,
在Rt△CC1B中,CC1=4,BC=2,∴BC1=2
,
设C到BC1的距离为d,由于BC•CC1=BC1•d,
∴d=
,HI=
,
在Rt△DHI中,HI=
,DH=2,∴DI=
=
,
∴cos∠DIH=
=
=
,
∴二面角C-BC1-D的余弦值为
.
 解:(1)证明:∵D是棱AA1的中点,∴A1D=AD=2,
解:(1)证明:∵D是棱AA1的中点,∴A1D=AD=2,在Rt△DAC中,AC=AD=2,∴∠ADC=45°,
同理,∠A1DC1=45°,∴∠CDC1=90°,∴DC⊥DC1,
又DB⊥DC1,∴DC1⊥面BCD,
∴DC1⊥BC.
(2)解:在直三棱柱ABC-A1B1C1中,CC1⊥BC,
由(1)得DC1⊥BC,∴BC⊥ACC1A1,∴面DCC1⊥面BCC1,
过D作DH⊥CC1于H,过H作HI⊥BC1于I,
则∠DIH为所求二面角的平面角,
在Rt△CC1B中,CC1=4,BC=2,∴BC1=2
| 5 |
设C到BC1的距离为d,由于BC•CC1=BC1•d,
∴d=
| 4 | ||
|
| 2 | ||
|
在Rt△DHI中,HI=
| 2 | ||
|
| DH2+HI2 |
2
| ||
|
∴cos∠DIH=
| HI |
| DI |
| ||||||
|
| ||
| 6 |
∴二面角C-BC1-D的余弦值为
| ||
| 6 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知下列各组命题,其中p是q的充分必要条件的是( )
| A、p:m≤-2或m≥6;q:y=x2+mx+m+3 有两个不同的零点 | ||
B、p:
| ||
| C、p:cosα=cosβ;q:tanα=tanβ | ||
| D、p:A∩B=A; q:A⊆U,B⊆U,∁UB⊆∁UA |
已知全集U=R,A={x|x≤a+2},B={x|x≥a2},若∁U(A∩B)=R,则a的取值范围是( )
| A、[-1,2] |
| B、(-1,2) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1)∪(2,+∞) |
如图是一个空间几何体的三视图,如果直角三角形边长均为1,那么几何体体积为( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
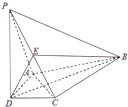 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2 如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )
如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )