题目内容
已知x∈（0，
），则y=x
的最大值为（ ）
| 1 |
| 4 |
| 1-4x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式即可得出．
解答：
解：∵x∈（0，
），
∴y=x
=
≤
=
，当且仅当x=
时取等号．
∴y=x
的最大值为
．
故选：C．
| 1 |
| 4 |
∴y=x
| 1-4x |
|
|
| ||
| 18 |
| 1 |
| 6 |
∴y=x
| 1-4x |
| ||
| 18 |
故选：C．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
如图所示为一简谐振动的图象，则下列判断正确的是（ ）
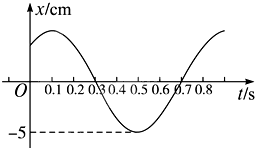
| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |
已知sinα=
，则cos4α的值是（ ）
| ||
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若θ为锐角，求y=3cosθ•sin2θ的最大值是（ ）
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、1 |
已知条件p：x2-2x-3＜0，条件q：x＞a，若p是q的充分不必要条件，则a的取值范围为（ ）
| A、a＞3 | B、a≥3 |
| C、a＜-1 | D、a≤-1 |
已知tan（π-a）=2，则
=（ ）
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若m=（x+3）（x+7），n=（x+4）（x+6），则m，n的大小关系为（ ）
| A、m＜n | B、m=n |
| C、m＞n | D、不确定 |