题目内容
17.已知集合A={x|x2-9x+14=0},集合B={x|ax+2=0},若B?A,则实数a的取值集合为$\left\{{-1,-\frac{7}{2},0}\right\}$.分析 先确定集合A={2,7},然后利用B⊆A,得到集合B的元素和A的关系,分类讨论,即可得出结论.
解答 解:A={x|x2-9x+14=0}={2,7},因为B⊆A,
所以若a=0,即B=∅时,满足条件.
若a≠0,则B={-$\frac{2}{a}$},
若B⊆A,则-$\frac{2}{a}$=2或-7,解得a=-1或-$\frac{7}{2}$.
则实数a的取值的集合为$\left\{{-1,-\frac{7}{2},0}\right\}$.
故答案为:$\left\{{-1,-\frac{7}{2},0}\right\}$.
点评 本题主要考查集合关系的应用,注意当B为空集时,也满足条件,防止漏解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
7.用反证法证明“a+b$\sqrt{2}$(a、b∈Z)是无理数”时,假设正确的是( )
| A. | 假设$\sqrt{2}$是有理数 | B. | 假设b$\sqrt{2}$(b∈Z)是有理数 | ||
| C. | 假设a+$\sqrt{2}$(a∈Z)是有理数 | D. | 假设a+b$\sqrt{2}$(a、b∈Z)是有理数 |
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.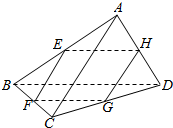 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.