题目内容
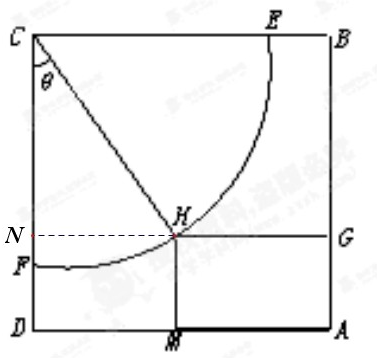
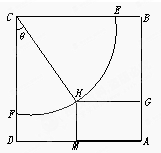 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?考点:三角函数中的恒等变换应用,三角函数的最值
专题:应用题,三角函数的求值,三角函数的图像与性质
分析:延长GH交CD于N,则NH=40sinθ,CN=40cosθ.将面积表示为S=(50-40cosθ)(50-40sinθ).利用三角函数的性质化简并利用二次函数求出最值.从而解得本题
解答:
解:延长GH交CD于N,则NH=40sinθ,CN=40cosθ.
∴HM=ND=50-40cosθ.AM=50-40sinθ.
∴S=(50-40cosθ)(50-40sinθ)
=100[25-20(sinθ+cosθ)+16sinθcosθ],(0≤θ≤
)
令t=sinθ+cosθ=
sin(θ+
),
则sinθcosθ=
,且t∈[1,
].
∴S=100[25-20t+8(t2-1)]
=800(t-
)2+450.
又∵t∈[1,
],
∴当t=1时,S取最大值500.
此时,
sin(θ+
)=1,
∴sin(θ+
)=
.
∵
≤θ+
≤
,
∴θ+
=
或
即θ=0或θ=
.
答:当点H在
的端点E或F处时,该健身室的面积最大,最大面积为500m2.
∴HM=ND=50-40cosθ.AM=50-40sinθ.
∴S=(50-40cosθ)(50-40sinθ)
=100[25-20(sinθ+cosθ)+16sinθcosθ],(0≤θ≤
| π |
| 2 |

令t=sinθ+cosθ=
| 2 |
| π |
| 4 |
则sinθcosθ=
| t2-1 |
| 2 |
| 2 |
∴S=100[25-20t+8(t2-1)]
=800(t-
| 5 |
| 4 |
又∵t∈[1,
| 2 |
∴当t=1时,S取最大值500.
此时,
| 2 |
| π |
| 4 |
∴sin(θ+
| π |
| 4 |
| ||
| 2 |
∵
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴θ+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
即θ=0或θ=
| π |
| 2 |
答:当点H在
 |
| EF |
点评:本题考查三角函数的图象和性质,函数求最值等知识的综合运用.属于中档题.

练习册系列答案
相关题目
如果cos(π+A)=-
,那么sin(π+A)=( )
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|