题目内容
已知{(x,y)|(3+m)x+y=3m-4}∩{(x,y)|7x+(5-m)y=8}=Φ,则直线(3+m)x+y=3m+4与坐标轴所围成的三角形的面积为 .
考点:定积分
专题:直线与圆
分析:根据{(x,y)|(3+m)x+y=3m-4}∩{(x,y)|7x+(5-m)y=8}=Φ得到两直线平行,然后根据直线平行的等价条件求出m的值,即可得到结论.
解答:
解:∵{(x,y)|(3+m)x+y=3m-4}∩{(x,y)|7x+(5-m)y=8}=Φ,
∴(3+m)x+y=3m-4与7x+(5-m)y=8平行,
则当m=-3时,两直线等价为y=-13m或7x+8y=8,两直线不平行,
当m≠-3时,若两直线平行,则
=
,
即m2-2m-8=0,解得m=-2或m=4,
当m=-2时,两直线等价为x+y=-10或7x+7y=8,两直线平行,
当m=4时,两直线等价为7x+y=8或7x+y=8,此时两直线重复,不成立.
∴m=-2,
此时直线(3+m)x+y=3m+4为x+y=-2,
当x=0时,y=-2,
当y=0时,x=-2,
∴直线(3+m)x+y=3m+4与坐标轴所围成的三角形的面积为
×2×2=2,
故答案为:2.
∴(3+m)x+y=3m-4与7x+(5-m)y=8平行,
则当m=-3时,两直线等价为y=-13m或7x+8y=8,两直线不平行,
当m≠-3时,若两直线平行,则
| 7 |
| 3+m |
| 5-m |
| 1 |
即m2-2m-8=0,解得m=-2或m=4,
当m=-2时,两直线等价为x+y=-10或7x+7y=8,两直线平行,
当m=4时,两直线等价为7x+y=8或7x+y=8,此时两直线重复,不成立.
∴m=-2,
此时直线(3+m)x+y=3m+4为x+y=-2,
当x=0时,y=-2,
当y=0时,x=-2,
∴直线(3+m)x+y=3m+4与坐标轴所围成的三角形的面积为
| 1 |
| 2 |
故答案为:2.
点评:本题主要考查直线平行的应用,以及三角形面积的计算,根据条件求出m的值是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)=2sinxcosx-2cos2x,则函数y=f(x)的图象的一个对称中心为( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
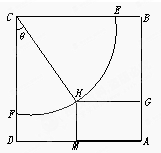 某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),ABCD是一块边长为50m的正方形地皮,扇形CEF是运动场的一部分,其半径为40m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在何处时,该健身室的面积最大,最大面积是多少?