题目内容
记关于x的不等式x-
<0的解集为S,不等式|x-1|<1的解集为T.
(1)若a=1,求S∪T,S∩T;
(2)若S⊆T,求a的取值范围.
| a |
| x |
(1)若a=1,求S∪T,S∩T;
(2)若S⊆T,求a的取值范围.
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:(1)由题意,代入a=1求出集合S、T,再求S∪T,S∩T;
(2)由题意,无论a取何值,当x→-∞时,x-
<0一定会成立,故无解.
(2)由题意,无论a取何值,当x→-∞时,x-
| a |
| x |
解答:
解:(1)若a=1,则x-
<0,
解得,x∈(-∞,-1)∪(0,1),
故S=(-∞,-1)∪(0,1);
解|x-1|<1得,
0<x<2,
故T=(0,2),
则S∪T=(-∞,-1)∪(0,2);
S∩T=(0,1);
(2)无论a取何值,
当x→-∞时,x-
<0一定会成立,
故S⊆T不可能成立.
| 1 |
| x |
解得,x∈(-∞,-1)∪(0,1),
故S=(-∞,-1)∪(0,1);
解|x-1|<1得,
0<x<2,
故T=(0,2),
则S∪T=(-∞,-1)∪(0,2);
S∩T=(0,1);
(2)无论a取何值,
当x→-∞时,x-
| a |
| x |
故S⊆T不可能成立.
点评:本题考查了集合的运算,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若点(-1,m)在直线x+2y-1=0的上方,则y=
( )
| m2+1 |
| m-1 |
A、有最小值2+2
| ||
B、有最大值2+2
| ||
C、有最大值2-2
| ||
D、有最小值2
|
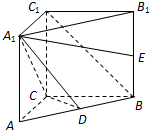 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=