题目内容
17.根据条件求抛物线的标准方程.(1)抛物线的顶点在原点,以坐标轴为对称轴,且焦点在直线x+y+2=0上;
(2)抛物线的顶点在原点,焦点是圆x2十y2-4x=0的圆心.
分析 (1)求出已知直线与坐标轴的交点A和B,在焦点分别为A和B的情况下设出抛物线标准方程,对照抛物线焦点坐标的公式求待定系数,即可得到相应抛物线的方程.
(2)抛物线顶点在原点,圆x2十y2-4x=0的圆心是抛物线的焦点,故先求咄圆心,再求抛物线的方程即可.
解答 解:(1)直线x+y+2=0交x轴于点A(-2,0),与y轴交于点B(0,-2);
①当抛物线的焦点在A点时,设方程为y2=-2px,(p>0),可得2p=8,
∴抛物线方程为y2=-8x;
②当抛物线的焦点在B点时,设方程为x2=-2p'y,(p'>0),可得2p'=8,
∴抛物线方程为x2=-8y
综上所述,得此抛物线方程为y2=-8x或x2=8y;
(2)由圆的方程x2十y2-4x=0,即(x-2)2+y2=4可知,圆心为F(2,0),
半径为2,又由抛物线焦点为已知圆的圆心,得到抛物线焦点为F(2,0),
抛物线方程为y2=8x.
点评 本题给出抛物线的焦点坐标,求它的标准方程,着重考查了抛物线的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
2.下面几个空间图形中,虚线、实线使用不正确的有( )
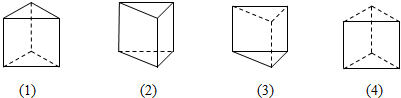

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |
