题目内容
已知数列{an}为等差数列,a5=5,d=1;数列{bn}为等比数列,b4=16,q=2.
(1)求数列{an}、{bn}的通项公式an、bn;
(2)设cn=an+bn,求数列{cn}的前n项和为Tn.
(1)求数列{an}、{bn}的通项公式an、bn;
(2)设cn=an+bn,求数列{cn}的前n项和为Tn.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式,求出首项,由此能求出an=n;由已知条件利用等比数列通项公式,求出首项,由此能求出bn=2n.
(2)由cn=an+bn=n+2n,利用分组求和法能求出数列{cn}的前n项和Tn.
(2)由cn=an+bn=n+2n,利用分组求和法能求出数列{cn}的前n项和Tn.
解答:
解:(1)∵数列{an}为等差数列,a5=5,d=1,
∴a1+4=5,解得a1=1,
∴an=1+(n-1)×1=n.
∵数列{bn}为等比数列,b4=16,q=2,
∴b1•23=16,解得b1=2,
∴bn=2×2n-1=2n.
(2)∵cn=an+bn=n+2n,
∴Tn=(1+2+3+…+n)+(2+22+23+…+2n)
=
+
=
+2n+1-2.
∴a1+4=5,解得a1=1,
∴an=1+(n-1)×1=n.
∵数列{bn}为等比数列,b4=16,q=2,
∴b1•23=16,解得b1=2,
∴bn=2×2n-1=2n.
(2)∵cn=an+bn=n+2n,
∴Tn=(1+2+3+…+n)+(2+22+23+…+2n)
=
| n(n+1) |
| 2 |
| 2(1-2n) |
| 1-2 |
=
| n2+n |
| 2 |
点评:本题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查抽象概括能力,推理论证能力,运算求解能力,考查化归与转化思想、函数与方程思想.

练习册系列答案
相关题目
观察下面频率等高条形图,其中两个分类变量C之间关系最强的是( )
A、 |
B、 |
C、 |
D、 |
在区间[0,π]上随机取一个实数x,使得sinx∈[0,
]的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若α表示平面,a,b表示直线,给定下列四个说法:其中正确说法的序号是( )
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
①若a∥α,a⊥b,则b⊥α;
②若a∥b,a⊥α,则b⊥α;
③若a⊥α,a⊥b,则b∥α;
④若a⊥α,b⊥α,则a∥b.
| A、①和② | B、②和④ |
| C、③和④ | D、①和③ |
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )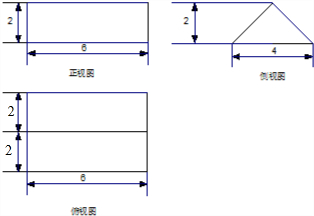

| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |
已知函数f(x)=(2k-1)x+2在R上是减函数,则实数k的取值范围为( )
A、k<-
| ||
B、k>-
| ||
C、k<
| ||
D、k>
|
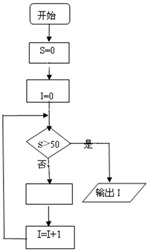 程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填
程序框图,如图所示为1+2+3+…+n>50的最小自然数n的程序框图,在空白框中应填