题目内容
已知函数f(x)=
,若f(a)=b,则f(-a)= .
| ex-e-x |
| ex+e-x |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由题意可得f(-x)=
=-
=-f(x),从而求得.
| e-x-ex |
| ex+e-x |
| ex-e-x |
| ex+e-x |
解答:
解:f(-x)=
=-
=-f(x),
故由f(a)=b得,
f(-a)=-b;
故答案为:-b.
| e-x-ex |
| ex+e-x |
| ex-e-x |
| ex+e-x |
故由f(a)=b得,
f(-a)=-b;
故答案为:-b.
点评:本题考查了函数的奇偶性的判断与应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
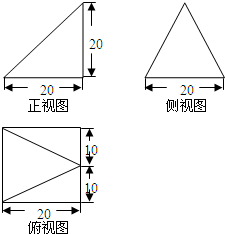 已知某个几何体的三视图如图,根据图中标出 的尺寸(单位:cm),则此几何体的所有侧面的面积中最大的是( )
已知某个几何体的三视图如图,根据图中标出 的尺寸(单位:cm),则此几何体的所有侧面的面积中最大的是( )A、100
| ||
B、100
| ||
C、200
| ||
D、200
|
若x,y满足不等式组
,且y+
x的最大值为2,则实数m的值为( )
|
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
D、
|
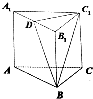 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.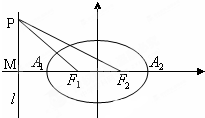 如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<
如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<