题目内容
已知向量
,
不共线,且
•
≠0,向量
=
•
-
,则向量
与
的夹角为 .
| a |
| b |
| a |
| b |
| c |
| ||||
|
| a |
| b |
| a |
| c |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:先进行
•
的运算,结果为0,因此夹角为直角.问题获解.
| a |
| c |
解答:
解:
•
=
•(
•
-
)=
•
•
-
•
=
•
-
•
=0,
∴
⊥
故向量
与
的夹角为
,
故答案为:
| a |
| c |
| a |
| ||||
|
| a |
| b |
| a |
| ||||
|
| a |
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| c |
故向量
| a |
| c |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题考查向量的数乘,向量的数量积,向量的运算律、及夹角.准确按照运算律计算是关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
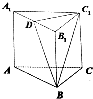 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,∠ACB=90°,D是AA1的中点.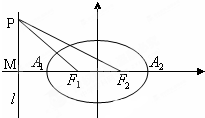 如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<
如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<