题目内容

11．若命题p：a=$\frac{2}{3}$，命题q：直线ax-2y=1与直线2x-6y=3平行，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 根据充分必要条件的定义结合两直线平行的性质判断即可．

解答 解：若“a=$\frac{2}{3}$”成立，则两直线的方程分别是2x-6y-3=0与2x-6y-3=0，两直线重合，不是充分条件，
反之，当“直线ax-2y-1=0与直线2x-6y-3=0平行”成立时，得a=$\frac{2}{3}$，经检验两直线重合，不是必要条件，
故选：D．

点评 本题考查了充分必要条件，考查直线平行的性质，是一道基础题．

练习册系列答案
相关题目
1．在△ABC中，角A，B，C的对边分别为a，b，c，c=5且b（2sinB+sinA）+（2a+b）sinA=2csinC．
（1）求C的值；
（2）若cosA=$\frac{4}{5}$，求b的值．
2．函数y=0.75sin（x+$\frac{π}{4}$）（x∈[-π，π]）的递减区间是[-π，-$\frac{3π}{4}$]，[$\frac{π}{4}$，π]；
函数y=$\sqrt{3}$cos（$\frac{1}{2}$x+$\frac{2π}{3}$）（x∈[0，2π]）的递增区间是[$\frac{2π}{3}$，2π]；
函数y=$\frac{3}{5}$sin（3x-$\frac{π}{6}$）（x∈R）的递增区间是[-$\frac{π}{9}$+$\frac{2kπ}{3}$，$\frac{2π}{9}$+$\frac{2kπ}{3}$]，k∈Z．
19．设数列{an}满足：an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$，a2015=3，那么a1等于（　　）
A．$\frac{1}{2}$B．2C．-$\frac{1}{3}$D．3
6．已知函数f（x）=ax2-2ax+1+b（a＞0）
（1）若f（x）在区间[2，3]上的最大值为4、最小值为1，求a，b的值；
（2）若a=1，b=1，关于x的方程f（|2x-1|）+k（4-3|2x-1|）=0，有3个不同的实数解，求实数k的值．
16．等差数列{an}满足a3=-3，a10=11．
（1）求{an}的通项公式；
（2）令bn=$\frac{2n}{{a}_{n}}$，求{bn}的最大项和最小项的值．
3．己知f（n）=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{n^2}$．则（　　）
A．f（n）中共有n项，当n=2时，f（2）=$\frac{1}{2}$+$\frac{1}{3}$
B．f（n）中共有n+1项，当n=2时，f（2）=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$
C．f（n）中共有n2-n项，当n=2时，f（2）=$\frac{1}{2}$+$\frac{1}{3}$
D．f（n）中共有n2-n+1项，当n=2时，f（2）=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$
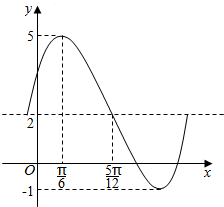20．已知函数f（x）=Asin（ωx+φ）+b（A＞0，ω＞0，0＜φ＜π，b为常数）的一段图象如图所示．
（1）求函数f（x）的解析式；
（2）函数f（x）在y轴右侧的极小值点的横坐标组成数列{an}，设右侧的第一个极小值点的横坐标为首项为a1，试求数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Sn．
7．已知$\overrightarrow{m}$=（1，cosx），$\overrightarrow{n}$=（t，$\sqrt{3}$sinx-cosx），函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$（t∈R）的图象经过点M（$\frac{π}{12}$，0）．
（Ⅰ）求t的值以及函数f（x）的最小正周期和单调增区间；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，若a=$\frac{cosB+bcosC}{2cosB}$，求f（A）的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网