题目内容
1.在△ABC中,角A,B,C的对边分别为a,b,c,c=5且b(2sinB+sinA)+(2a+b)sinA=2csinC.(1)求C的值;
(2)若cosA=$\frac{4}{5}$,求b的值.
分析 (1)利用正弦定理化简已知等式可得(2b+a)b+(2a+b)a=2c2,化简可得:a2+b2-c2=-ab,利用余弦定理可求cosC=-$\frac{1}{2}$,结合范围C∈(0,π),即可求得C的值.
(2)由已知,利用同角三角函数基本关系式可求sinA,利用两角和的正弦函数公式即可求得sinB=sin(A+C)的值,由正弦定理即可计算求得b=$\frac{csinB}{sinC}$的值.
解答 (本题满分为12分)
解:(1)∵b(2sinB+sinA)+(2a+b)sinA=2csinC.
∴(2b+a)b+(2a+b)a=2c2,…2分
化简可得:a2+b2-c2=-ab,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$,…4分
∵C∈(0,π),
∴C=$\frac{2π}{3}$…6分
(2)∵cosA=$\frac{4}{5}$,A∈(0,π),
∴sinA=$\frac{3}{5}$,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{3}{5}×(-\frac{1}{2})+\frac{4}{5}×\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}-3}{10}$,…10分
∴由正弦定理可得:b=$\frac{csinB}{sinC}$=$\frac{5×\frac{4\sqrt{3}-3}{10}}{\frac{\sqrt{3}}{2}}$=4$-\sqrt{3}$.…12分
点评 本题主要考查了正弦定理,余弦定理,两角和与差的三角函数公式等基础知识,考查了运算求解能力,考查了化归与转化思想的应用,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.函数$y={log_{\frac{1}{4}}}({-{x^2}+2x+3})$的单调增区间是( )
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
12.$\frac{3+2i}{2-3i}$=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
10.设等差数列{an}的前n项和为Sn,若S6=9,S12=36,则a13+a14+…+a18=( )
| A. | 63 | B. | 45 | C. | 36 | D. | 27 |
11.若命题p:a=$\frac{2}{3}$,命题q:直线ax-2y=1与直线2x-6y=3平行,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
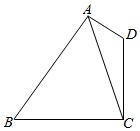 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.