题目内容
9.设x,y满足约束条件$\left\{\begin{array}{l}8x-y-4≤0\\ x+y+1≥0\\ y-4x≤0\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为2,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 9 |
分析 先根据条件画出可行域,设z=ax+by,再利用几何意义求最值,将最大值转化为y轴上的截距,只需求出直线z=ax+by,过可行域内的点(1,4)时取得最大值,从而得到一个关于a,b的等式,最后利用基本不等式求最小值即可
解答 解:不等式表示的平面区域如图所示阴影部分,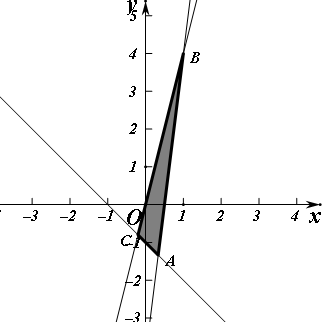
当直线ax+by=z(a>0,b>0)过直线8x-y-4=0与y=4x的交点B(1,4)时,
目标函数z=ax+by(a>0,b>0)取得最大2,
即a+4b=2,
则$\frac{1}{a}+\frac{1}{b}$=$\frac{1}{2}$(a+4b)($\frac{1}{a}+\frac{1}{b}$)=$\frac{1}{2}$(5+$\frac{4b}{a}+\frac{a}{b}$)$≥\frac{1}{2}$(5+4)=$\frac{9}{2}$;
当且仅当a=2b时等号成立;
故选:C.
点评 本题主要考查了基本不等式在最值问题中的应用、简单的线性规划,以及利用几何意义求最值,属于中档题.

练习册系列答案
相关题目
20.已知集合A={x∈N|x2+3x-10≤0},则集合A中元素的个数为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
17.已知抛物线x2=4y的焦点是F,直线$x-\sqrt{3}y+\sqrt{3}=0$交抛物线于A,B两点,且|AF|>|BF|,则$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
4.下列关于命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| C. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m.”为真命题 | |
| D. | 若命题P:?n∈N,2n>1000,则¬P:?n∈N,2n>1000 |
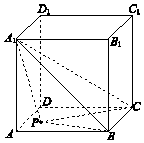 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.