题目内容
1.某种商品价格与该商品日需求量之间的几组对照数据如表:| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程y=bx+a,其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
分析 (1)根据回归系数公式计算回归系数,得出回归方程;
(2)把x=40,代入回归方程解出y即可.
解答 解:(1)$\overline{x}$=20,$\overline{y}$=8,
∴b=$\frac{110+150+160+150+150-5×20×8}{100+225+400+625+900-5×2{0}^{2}}$=-0.32,a=8-(-0.32)×20=14.4,
∴线性回归方程为y=-0.32x+14.4;
(2)当价格x=40元/kg时,y=-0.32x+14.4=1.6kg,即日需求量y的预测值为1.6kg.
点评 本题考查线性回归方程,是一个基础题,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错.

练习册系列答案
相关题目
17.已知抛物线x2=4y的焦点是F,直线$x-\sqrt{3}y+\sqrt{3}=0$交抛物线于A,B两点,且|AF|>|BF|,则$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
6.若a为实数,$\frac{2+ai}{1+i}$=-2i,则a等于( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
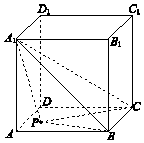 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$. 如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.
如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点. 在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.
在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.