题目内容
4．已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ x≤1\end{array}\right.$，则z=2x-y的最小值是（ ）| A． | -1 | B． | 1 | C． | -3 | D． | 2 |
分析 由线性约束条件画出可行域，然后求出目标函数的最小值．
解答 解：画出实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ x≤1\end{array}\right.$可行域，z=2x-y经过可行域的A时，目标函数取得最小值，
直线x-y+2=0与直线x+y=0的交点A（-1，1）处，
目标函数z=2x-y的最小值为-3．
故选：C．
点评 本题考查不等式组所表示的平面区域和简单的线性规划问题．在线性规划问题中目标函数取得最值的点一定是区域的顶点和边界，在边界上的值也等于在这个边界上的顶点的值，故在解答选择题或者填空题时，只要能把区域的顶点求出，直接把顶点坐标代入进行检验即可．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20．已知集合A={x∈N|x2+3x-10≤0}，则集合A中元素的个数为（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
1．某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从1～1000进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为（ ）
| A． | 16 | B． | 17 | C． | 18 | D． | 19 |
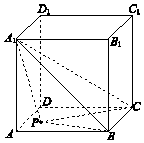如图，正方体ABCD-A1B1C1D1的棱长为2，点P在正方形ABCD的边界及其内部运动．平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成，则W的面积是$\frac{π}{4}$；四面体P-A1BC的体积的最大值是$\frac{4}{3}$．
如图，已知四边形ABCD为正方形，四边形ABEF，四边形DCEF为菱形，且∠AFE=$\frac{π}{3}$，M为BC的中点．
在等腰Rt△ABC中，∠BAC=90°，腰长为2，D、E分别是边AB、BC的中点，将△BDE沿DE翻折，得到四棱锥B-ADEC，且F为棱BC中点，BA=$\sqrt{2}$．
14．已知集合$A=\{x|\frac{x-2}{x+1}≤0，x∈Z\}$，B={1，2，3}，则A∩B=（ ）
| A． | {1} | B． | {1，2} | C． | {0，1，2，3} | D． | {-1，0，1，2，3} |