题目内容
13.若$cosα=\frac{3}{5},α∈(0,\frac{π}{2})$,则s$in(α-\frac{π}{6})$的值为$\frac{{4\sqrt{3}-3}}{10}$.分析 由已知利用同角三角函数基本关系式可求sinα,进而利用两角和与差的正弦函数即可计算.
解答 解:∵$cosα=\frac{3}{5},α∈(0,\frac{π}{2})$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4}{5}$,
∴s$in(α-\frac{π}{6})$=sinαcos$\frac{π}{6}$-cosαsin$\frac{π}{6}$=$\frac{4}{5}$×$\frac{\sqrt{3}}{2}$-$\frac{3}{5}$×$\frac{1}{2}$=$\frac{{4\sqrt{3}-3}}{10}$.
故答案是:$\frac{{4\sqrt{3}-3}}{10}$.
点评 本题主要考查了同角三角函数基本关系式,两角和与差的正弦公式,难度不大,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
3.一个袋中有大小相同,编号分别为1,2,3,4,5的五个球,从中有放回地每次取一个球,共取3次,取得三个球的编号之和不小于13的概率为( )
| A. | $\frac{4}{125}$ | B. | $\frac{7}{125}$ | C. | $\frac{2}{25}$ | D. | $\frac{4}{25}$ |
4.下列关于命题的说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| B. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| C. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m.”为真命题 | |
| D. | 若命题P:?n∈N,2n>1000,则¬P:?n∈N,2n>1000 |
1.某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为( )
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
8.已知A(3,-1),B=(x,y),C(0,1)三点共线,若x,y均为正数,则$\frac{3}{x}$+$\frac{2}{y}$的最小值是( )
| A. | $\frac{5}{3}$ | B. | $\frac{8}{3}$ | C. | 8 | D. | 24 |
17.已知数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,设Sn=a1+a2+…+an,则下列结论正确的是( )
| A. | a100=-a S100=2b-a | B. | a100=-b S100=2b-a | ||
| C. | a100=-b S100=b-a | D. | a100=-a S100=b-a |
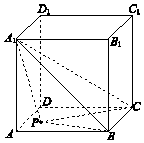 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$. 在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.
在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.