题目内容
已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时f(x)取得极值-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间和极大值.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间和极大值.
考点:利用导数研究函数的单调性,函数奇偶性的判断,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由f(-x)=-f(x)可得d=0,得f(x)=ax3+cx,求出f'(x),得方程组,解出即可;
(2)由f(x)=x3-3x得f'(x)=3x2-3,令f'(x)=0得x1=-1,x2=1,从而求出单调区间,进而求出极值.
(2)由f(x)=x3-3x得f'(x)=3x2-3,令f'(x)=0得x1=-1,x2=1,从而求出单调区间,进而求出极值.
解答:
解:(1)∵f(x)为奇函数,
∴由f(-x)=-f(x)可得d=0,
∴f(x)=ax3+cx…(2分)f'(x)=3ax2+c,
当x=1时f(x)取得极值-2,
则
,
解方程组得
,
故所求解析式为f(x)=x3-3x.
(2)由f(x)=x3-3x得f'(x)=3x2-3,
令f'(x)=0得x1=-1,x2=1,
即增区间为(-∞,-1),(1,+∞),减区间(-1,1);
当x=-1时,函数有极大值2.
∴由f(-x)=-f(x)可得d=0,
∴f(x)=ax3+cx…(2分)f'(x)=3ax2+c,
当x=1时f(x)取得极值-2,
则
|
解方程组得
|
故所求解析式为f(x)=x3-3x.
(2)由f(x)=x3-3x得f'(x)=3x2-3,
令f'(x)=0得x1=-1,x2=1,
即增区间为(-∞,-1),(1,+∞),减区间(-1,1);
当x=-1时,函数有极大值2.
点评:本题考查了函数的单调性,导数的应用,函数的极值问题,是的基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
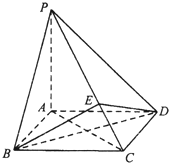 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,PA=AD=AB=2BC,M是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,PA=AD=AB=2BC,M是PC的中点.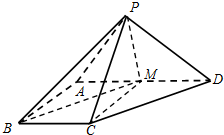 如图,四棱锥P-ABCD中,AB⊥AD,AD∥BC,AD=2,AB=BC=1,PA=PD=
如图,四棱锥P-ABCD中,AB⊥AD,AD∥BC,AD=2,AB=BC=1,PA=PD=