题目内容
已知等差数列{an}及等比数列{bn},其中b1=1,公比q<0,且数列{an+bn}的前三项分别为2、1、4.
(Ⅰ)求an及q;
(Ⅱ)求数列{an+bn}的前n项和Pn.
(Ⅰ)求an及q;
(Ⅱ)求数列{an+bn}的前n项和Pn.
考点:数列的求和,等差数列的通项公式,等比数列的通项公式
专题:计算题,等差数列与等比数列
分析:(Ⅰ)利用数列{an+bn}的前三项分别为2、1、4,建立方程,即可求an及q;
(Ⅱ)利用分组求和,即可求数列{an+bn}的前n项和Pn.
(Ⅱ)利用分组求和,即可求数列{an+bn}的前n项和Pn.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,首项为a1,则
∵数列{an+bn}的前三项分别为2、1、4,
∴a1+1=2,a1+d+q=1,a1+2d+q2=4,
∴a1=1,q=-1或3,
∵q<0,
∴q=-1,d=1,
∴an=n;
(Ⅱ)等差数列{an}的前n项和为
,等比数列{bn}}的前n项和为
,
∴n为偶数时,Pn=
;n为奇数时,Pn=
+1.
∵数列{an+bn}的前三项分别为2、1、4,
∴a1+1=2,a1+d+q=1,a1+2d+q2=4,
∴a1=1,q=-1或3,
∵q<0,
∴q=-1,d=1,
∴an=n;
(Ⅱ)等差数列{an}的前n项和为
| n(n+1) |
| 2 |
| 1-(-1)n |
| 2 |
∴n为偶数时,Pn=
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
点评:本题主要考查等差数列的定义及数列求和的方法,考查学生的运算求解能力,属中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
不等式x2-4x-12>0的解集是( )
| A、{x|x<-5或x>3} |
| B、{x|-5<x<3} |
| C、{x|-2<x<6} |
| D、{x|x<-2或x>6} |
设f(x)=
,则f(f(-2))=( )
|
| A、2 | B、-2 | C、4 | D、-4 |
 如图所示,正四棱柱ABCD-A1B1C1D1中底面边长为
如图所示,正四棱柱ABCD-A1B1C1D1中底面边长为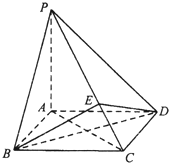 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.