题目内容
已知A(2,0),B(0,2),C(cosθ,sinθ),O为坐标原点.
(1)
•
=-
,求sin2θ的值;
(2)若|
+
|=
,且θ∈(-π,0),求
与
的夹角.
(1)
| AC |
| BC |
| 1 |
| 3 |
(2)若|
| OA |
| OC |
| 7 |
| OB |
| OC |
考点:平面向量数量积的运算
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用平面向量的数量积,结合三角函数的恒等公式,即可求出结果;
(2)利用平面向量的数量积表示出模长,结合三角函数的恒等式,平面向量的数量积,即可求出向量的夹角.
(2)利用平面向量的数量积表示出模长,结合三角函数的恒等式,平面向量的数量积,即可求出向量的夹角.
解答:
解:(1)∵
=(cosθ,sinθ)-(2,0)=(cosθ-2,sinθ),
=(cosθ,sinθ)-(0,2)=(cosθ,sinθ-2),
∴
•
=cosθ(cosθ-2)+sinθ(sinθ-2)=1-2(sinθ+cosθ)=-
,…(3分)
∴sinθ+cosθ=
,
∴两边平方,整理得,
sin2θ=-
;…(5分)
(2)∵
=(2,0),
(cosθ,sinθ),
∴
+
=(2+cosθ,sinθ),
∴|
+
|=
=
,
即4+4cosθ+cos2θ+sin2θ=7,
∴cosθ=
;
又θ∈(-π,0),∴θ=-
;…(7分)
又
=(0,2),
=(
,-
),
∴cos<
,
>=
=
=-
,
∴
与
的夹角<
,
>=
.…(10分)
| AC |
| BC |
∴
| AC |
| BC |
| 1 |
| 3 |
∴sinθ+cosθ=
| 2 |
| 3 |
∴两边平方,整理得,
sin2θ=-
| 5 |
| 9 |
(2)∵
| OA |
| OC |
∴
| OA |
| OC |
∴|
| OA |
| OC |
| (2+cosθ)2+sin2θ |
| 7 |
即4+4cosθ+cos2θ+sin2θ=7,
∴cosθ=
| 1 |
| 2 |
又θ∈(-π,0),∴θ=-
| π |
| 3 |
又
| OB |
| OC |
| 1 |
| 2 |
| ||
| 2 |
∴cos<
| OB |
| OC |
| ||||
|
|
0-
| ||
| 2×1 |
| ||
| 2 |
∴
| OB |
| OC |
| OB |
| OC |
| 5π |
| 6 |
点评:本题考查了平面向量的数量积的应用问题,也考查了三角函数的恒等式的应用问题,是综合性的运算题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,正四棱柱ABCD-A1B1C1D1中底面边长为
如图所示,正四棱柱ABCD-A1B1C1D1中底面边长为 2003年伊拉克战争初期,美英联军为了准确分析战场形势,有分别位于科威特和沙特的两个距离为
2003年伊拉克战争初期,美英联军为了准确分析战场形势,有分别位于科威特和沙特的两个距离为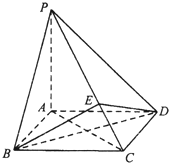 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,PA=AD=AB=2BC,M是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠BAD=90°,PA=AD=AB=2BC,M是PC的中点. 省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.