题目内容
甲、乙两人参加某种选拔测试．在备选的10道题中，甲答对其中每道题的概率都是
，乙能答对其中的5道题．规定每次考试都从备选的10道题中随机抽出3道题进行测试，答对一题加10分，答错一题（不答视为答错）减5分，至少得15分才能入选．
（Ⅰ）分别求甲得0分和乙得0分的概率；
（Ⅱ）求甲、乙两人中至少有一人入选的概率．
| 3 |
| 5 |
（Ⅰ）分别求甲得0分和乙得0分的概率；
（Ⅱ）求甲、乙两人中至少有一人入选的概率．
考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题：计算题,概率与统计
分析：（Ⅰ）根据答对一题加10分，答错一题（不答视为答错）减5分，可得甲得0分和乙得0分的概率；
（Ⅱ）由已知甲、乙至少答对2题才能入选，求出甲、乙入选的概率，利用对立事件，即可求得结论．
（Ⅱ）由已知甲、乙至少答对2题才能入选，求出甲、乙入选的概率，利用对立事件，即可求得结论．
解答：
解：（Ⅰ）甲得0分的概率为
×
×(1-
)2=
；乙得0分的概率为
=
；
（Ⅱ）由已知甲、乙至少答对2题才能入选，记甲入选为事件A，乙入选为事件B．
则P（A）=
×(
)2×
+(
)3=
，P（B）=
+
=
，
故甲乙两人至少有一人入选的概率P=1-P（
）=
．
| C | 1 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 36 |
| 125 |
| ||||
|
| 5 |
| 12 |
（Ⅱ）由已知甲、乙至少答对2题才能入选，记甲入选为事件A，乙入选为事件B．
则P（A）=
| C | 2 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 81 |
| 125 |
| 5 |
| 12 |
| 1 |
| 12 |
| 1 |
| 2 |
故甲乙两人至少有一人入选的概率P=1-P（
. |
| A |
. |
| B |
| 103 |
| 125 |
点评：本题考查概率的计算，考查互斥事件的概率，考查学生的计算能力，属于中档题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
2003年伊拉克战争初期，美英联军为了准确分析战场形势，有分别位于科威特和沙特的两个距离为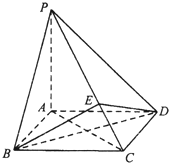
如图所示，四棱锥P-ABCD中，底面ABCD为正方形，PA=AD=1，PA⊥面ABCD，E为线段PC上靠近D的一个三等分点．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，∠BAD=90°，PA=AD=AB=2BC，M是PC的中点．