题目内容
已知数列{an}的前n项和为Sn,且a1=
,an+1=
an.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=n(2-Sn),n∈N*,若集合M={n|bn≥λ,n∈N*}恰有5个元素,求实数λ的取值范围.
| 1 |
| 2 |
| n+1 |
| 2n |
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=n(2-Sn),n∈N*,若集合M={n|bn≥λ,n∈N*}恰有5个元素,求实数λ的取值范围.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)由已知得
=
,结合等比数列的通项公式可求
,进而可求an
(2)由(1)知Sn=
+
+
+…+
,利用错位相减可求sn,然后利用数列的单调性可求bn的最大值与最小值,进而可求实数λ的取值范围
| an+1 |
| n+1 |
| 1 |
| 2 |
| an |
| n |
| an |
| n |
(2)由(1)知Sn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
解答:
解:(I)由已知得
=
,其中n∈N*
∴数列{
}是公比为
的等比数列,首项a1=
∴
=(
)n
∴an=
(2)由(1)知Sn=
+
+
+…+
,
Sn=
+
+
…+
,
两式相减可得,
Sn=
+
+
+…+
-
,
=
-
=1-
∴sn=2-
因此,bn=
,bn+1-bn=
-
=
所以,当n=1,b2-b1>0即b2>b1,
n>2时,bn+1-bn<0即bn+1-bn<0b1=
,b2=2,b3=
,b4=
,b5=
,b6=
要使得集合M有5个元素,实数λ的取值范围为
<λ≤
.
| an+1 |
| n+1 |
| 1 |
| 2 |
| an |
| n |
∴数列{
| an |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| n |
| 1 |
| 2 |
∴an=
| n |
| 2n |
(2)由(1)知Sn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
两式相减可得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
=
| ||||
1-
|
| 1 |
| 2n+1 |
| n+2 |
| 2n+1 |
∴sn=2-
| n+2 |
| 2n |
因此,bn=
| n(n+2) |
| 2n |
| (n+1)(n+3) |
| 2n+1 |
| n(n+2) |
| 2n |
| -n2+3 |
| 2n+1 |
所以,当n=1,b2-b1>0即b2>b1,
n>2时,bn+1-bn<0即bn+1-bn<0b1=
| 3 |
| 2 |
| 15 |
| 8 |
| 3 |
| 2 |
| 35 |
| 32 |
| 3 |
| 4 |
要使得集合M有5个元素,实数λ的取值范围为
| 3 |
| 4 |
| 35 |
| 32 |
点评:本题主要考查了等比数列的定义及通项公式求解的应用,数列的错位相减求和方法的应用,及数列单调性在求解数列的最值求解中的应用,试题具有一定的综合性

练习册系列答案
相关题目
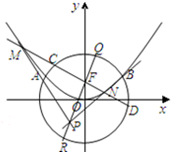 已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足
已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足