题目内容
已知a,b是实数,x=1是函数f(x)=2x3-3(a+1)x2+bx的一个极值点.
(Ⅰ)求a与b的关系;
(Ⅱ)对任意可取的实数a,当x∈[0,2]时,求证:2f(x)≤|3a-5|+3a+3.
(Ⅰ)求a与b的关系;
(Ⅱ)对任意可取的实数a,当x∈[0,2]时,求证:2f(x)≤|3a-5|+3a+3.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,根据x=1是函数f(x)=2x3-3(a+1)x2+bx的一个极值点,可得f′(1)=6-6(a+1)+b=0,△≠0,即可求a与b的关系;
(Ⅱ)记M为f(x)在x∈[0,2]上的最大值.分类讨论,求出M,即可证明结论.
(Ⅱ)记M为f(x)在x∈[0,2]上的最大值.分类讨论,求出M,即可证明结论.
解答:
(Ⅰ)解:∵f(x)=2x3-3(a+1)x2+bx,
∴f′(x)=6x2-6(a+1)x+b,
∵x=1是函数f(x)=2x3-3(a+1)x2+bx的一个极值点,
∴f′(1)=6-6(a+1)+b=0,△≠0,
∴b=6a,a≠1;
(Ⅱ)证明:f′(x)=6(x-a)(x-1),f(0)=0,f(2)=4,
记M为f(x)在x∈[0,2]上的最大值.
①a≤0时,M=f(2)=4,则有2f(x)≤2M=8=|3a-5|+3a+3;
②0<a<1时,M=max{f(a),f(2)},而f(a)=a2(3-a)<3a2<4,M=f(2)=4,则有2f(x)≤2M=8=|3a-5|+3a+3;
③1<a≤
时,M=max{f(1),f(2)},而f(1)=3a-1≤4,M=f(2)=4,则有2f(x)≤2M=8=|3a-5|+3a+3;
④
<a<2时,M=max{f(1),f(2)},而f(1)=3a-1>4,M=3a-1,则有2f(x)≤2M=6a-2=|3a-5|+3a+3;
⑤a≥2时,M=f(1)=3a-1,则有2f(x)≤2M=6a-2=|3a-5|+3a+3.
∴f′(x)=6x2-6(a+1)x+b,
∵x=1是函数f(x)=2x3-3(a+1)x2+bx的一个极值点,
∴f′(1)=6-6(a+1)+b=0,△≠0,
∴b=6a,a≠1;
(Ⅱ)证明:f′(x)=6(x-a)(x-1),f(0)=0,f(2)=4,
记M为f(x)在x∈[0,2]上的最大值.
①a≤0时,M=f(2)=4,则有2f(x)≤2M=8=|3a-5|+3a+3;
②0<a<1时,M=max{f(a),f(2)},而f(a)=a2(3-a)<3a2<4,M=f(2)=4,则有2f(x)≤2M=8=|3a-5|+3a+3;
③1<a≤
| 5 |
| 3 |
④
| 5 |
| 3 |
⑤a≥2时,M=f(1)=3a-1,则有2f(x)≤2M=6a-2=|3a-5|+3a+3.
点评:本题考查导数在最大值、最小值问题中的应用,考查利用导数研究函数的极值,考查学生分析解决问题的能力,有难度.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
设[x]表示不超过x的最大整数,如[1.5]=1,[-1.5]=-2,若函数f(x)=
,则函数g(x)=[f(x)]+[f(-x)]的值域为( )
| 1-ex |
| 1+ex |
| A、{-1} |
| B、{-1,0,1} |
| C、{0} |
| D、{-1,0} |
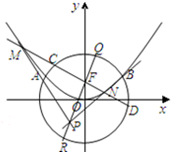 已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足
已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足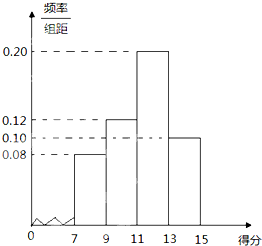 某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有
某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有