题目内容
已知:直线l的参数方程为
(t为参数),曲线C的参数方程为
(θ为参数).
(1)若在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求点Q到直线l的距离的最大值.
|
|
(1)若在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,
| π |
| 3 |
(2)设点Q是曲线C上的一个动点,求点Q到直线l的距离的最大值.
考点:参数方程化成普通方程
专题:计算题,坐标系和参数方程
分析:(1)把直线的参数方程化为普通方程,点的极坐标化为直角坐标即可作出判断;
(2)把曲线的参数方程化为普通方程可知为圆,然后由原定性质可求最大值;
(2)把曲线的参数方程化为普通方程可知为圆,然后由原定性质可求最大值;
解答:
解:(1)由直线l的参数方程为
消掉t,得y=
x+1,
由点P的极坐标为(4,
),得直角坐标(2,2
),
把x=2代入y=
x+1,得y=2
+1≠2
,
∴P不在直线l上;
(2)由曲线C的参数方程为
消掉θ,得(x-2)2+y2=1,
则曲线C为圆,圆心为(2,0),半径为1,
∴点Q到直线l的距离的最大值为:
+1=
+
.
|
| 3 |
由点P的极坐标为(4,
| π |
| 3 |
| 3 |
把x=2代入y=
| 3 |
| 3 |
| 3 |
∴P不在直线l上;
(2)由曲线C的参数方程为
|
则曲线C为圆,圆心为(2,0),半径为1,
∴点Q到直线l的距离的最大值为:
2
| ||||
|
| 3 |
| 3 |
| 2 |
点评:该题考查参数方程与普通方程的互化、极坐标与直角坐标的互化,属基础题,熟练进行相关方程间的转化是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示的流程图,若输出的结果是9,则判断框中的横线上可以填入的最大整数为( )
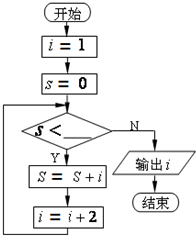

| A、17 | B、16 | C、15 | D、14 |
 如图,AE⊥平面DEC,四边形ABCD为正方形,M,N分别是线段BE、DE中点.
如图,AE⊥平面DEC,四边形ABCD为正方形,M,N分别是线段BE、DE中点.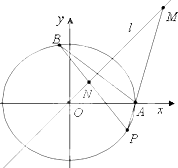 已知A(2,0),B(x0,y0)是椭圆C:
已知A(2,0),B(x0,y0)是椭圆C: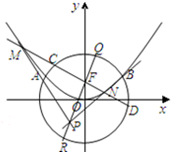 已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足
已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足