题目内容
8.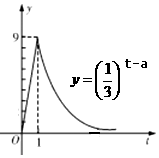 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(1)写出第一次服药后y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于$\frac{1}{9}$微克时,治疗有效,求服药一次后治疗有效的时间是多长?
分析 (1)根据图象,设$y=\left\{\begin{array}{l}{kt}&{0≤t≤1}\\{(\frac{1}{3})^{t-a}}&{t>1}\end{array}\right.$,根据t=1,y=9即可求出k和a,从而得出函数关系式y=f(t);
(2)根据y$≥\frac{1}{9}$即可求出t的取值范围,从而求出治疗有效的时间长.
解答 解:(1)设$y=\left\{\begin{array}{l}kt,0≤t≤1\\{({\frac{1}{3}})^{t-a}},t>1\end{array}\right.$,
当t=1时,由y=9得k=9,由${({\frac{1}{3}})^{1-a}}=9$得a=3;
∴$y=\left\{\begin{array}{l}9t,0≤t≤1\\{({\frac{1}{3}})^{t-3}},t>1\end{array}\right.$;
(2)由$y≥\frac{1}{9}$得$\left\{\begin{array}{l}0≤t≤1\\ 9t≥\frac{1}{9}\end{array}\right.$,或$\left\{\begin{array}{l}t>1\\{({\frac{1}{3}})^{t-3}}≥\frac{1}{9}\end{array}\right.$;
解得$\frac{1}{81}≤t≤5$;
∴服药一次后治疗有效的时间长是$5-\frac{1}{81}=4\frac{80}{81}$小时.
点评 考查分段函数的概念及表示,待定系数求函数解析式的方法,以及对数的运算.

练习册系列答案
相关题目
12.某手机厂商推出一款6寸大屏手机,现对500名该手机用户(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
(1)完成下列频率分布直方图,并指出女性用户和男性用户哪组评分更稳定(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |

(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取2名用户,求两名用户中评分都小于90分的概率.
18.已知集合P={-1,0,1},$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$,则P∩Q=( )
| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$. 如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.
如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.