题目内容
求证：对?x∈R，ex≥x+1．
考点：利用导数求闭区间上函数的最值
专题：导数的概念及应用
分析：首先构造函数f（x）=ex-x-1，然后求出函数的导数，利用导数与函数单调性的关系进行证明．
解答：
证明：设f（x）=ex-x-1，则f′（x）=ex-1，
∴当x=0时，f′（x）=0，f（x）=0．
当x＞0时，f′（x）＞0，
∴f（x）在（0，+∞）上是增函数，
∴f（x）＞f（0）=0．
当x＜0时，f′（x）＜0，
∴f（x）在（-∞，0）上是减函数，
∴f（x）＞f（0）=0．
∴对x∈R都有f（x）≥0，
∴ex≥x+1．
∴当x=0时，f′（x）=0，f（x）=0．
当x＞0时，f′（x）＞0，
∴f（x）在（0，+∞）上是增函数，
∴f（x）＞f（0）=0．
当x＜0时，f′（x）＜0，
∴f（x）在（-∞，0）上是减函数，
∴f（x）＞f（0）=0．
∴对x∈R都有f（x）≥0，
∴ex≥x+1．
点评：此题主要考查函数导数与函数单调性之间的关系，掌握并会熟练运用导数与函数单调性的关系．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知集合M={1，（m2-3m-1）+（m2-5m-6）i}，N={1，3}，M∩N={1，3}，则实数m的值为（ ）
| A、4 | B、-1 |
| C、4或-1 | D、1或6 |
已知圆x（x-1）+y（y-1）=0与圆x2+y2=r2（r＞
）相内切，则r等于（ ）
| 1 |
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
观察下列式子：1+
＜
，1+
+
＜
，1+
+
+
＜
，…，根据以上式子可以猜想：1+
+
+…+
＜（ ）
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20142 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知“整数对”按如下规律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第58个数对是（ ）
| A、（2，10） |
| B、（3，9） |
| C、（5，7） |
| D、（3，8） |
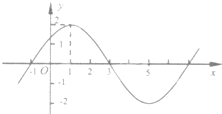已知函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜
如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD．求证：平面PDC⊥平面PAD．