题目内容
已知集合M={1,(m2-3m-1)+(m2-5m-6)i},N={1,3},M∩N={1,3},则实数m的值为( )
| A、4 | B、-1 |
| C、4或-1 | D、1或6 |
考点:复数相等的充要条件,交集及其运算
专题:计算题
分析:根据题意,由交集的定义可得3∈M,结合集合M,可得(m2-3m-1)+(m2-5m-6)i=3,进而由复数相等的意义,可得(m2-3m-1)=3且(m2-5m-6)=0,解可得m的值.
解答:
解:根据题意,若M∩N={1,3},则3∈M,
而M={1,(m2-3m-1)+(m2-5m-6)i},
则有(m2-3m-1)+(m2-5m-6)i=3,
即(m2-3m-1)=3且(m2-5m-6)=0,
解可得m=-1,
故选:B.
而M={1,(m2-3m-1)+(m2-5m-6)i},
则有(m2-3m-1)+(m2-5m-6)i=3,
即(m2-3m-1)=3且(m2-5m-6)=0,
解可得m=-1,
故选:B.
点评:本题考查复数的相等的充要条件以及集合交集的意义,关键是分析得到(m2-3m-1)+(m2-5m-6)i=3.

练习册系列答案
相关题目
若直线l经过原点和点(
,-1),则直线l的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知函数y=xf′(x)的图象如图所示,则y=f(x)的图象可能是( )


A、 |
B、 |
C、 |
D、 |
某校五四演讲比赛中,七位评委为一选手打出的分数如下:90,86,90,97,93,94,93,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A、92,2 |
| B、92,2.8 |
| C、93,2 |
| D、93,2.8 |
用数学归纳法证明“5n-2n能被3整除”的第二步中,n=k+1时,为了使用假设,应将5k+1-2k+1变形为( )
| A、5(5k-2k)+3×2k |
| B、(5k-2k)+4×5k-2k |
| C、(5-2)(5k-2k) |
| D、2(5k-2k)-3×5k |
函数y=log
sin(2x+
)的单调递减区间为( )
| 1 |
| 2 |
| π |
| 4 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
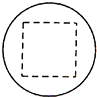 已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、64π | B、32π |
| C、16π | D、12π |
已知f(x+1)=
,f(1)=
(x∈N*)猜想f(x)的表达式为( )
| f(x) |
| f(x)+1 |
| 2 |
| 3 |
A、f(x)=
| ||
B、f(x)=
| ||
C、f(x)=
| ||
D、f(x)=
|