题目内容
19.已知双曲线x2-$\frac{{y}^{2}}{3}$=1的左、右焦点分别为F1、F2,P为双曲线右支上一点,点Q的坐标为(-2,3),则|PQ|+|PF1|的最小值为7.分析 依题意,可求得F1(-4,0),F2(4,0),P在双曲线的右支上,利用双曲线的定义|PF1|-|PF2|=4,可求得|PF1|=|PF2|+4,从而可求得|PF1|+|PQ|的最小值.
解答 解:由双曲线方程得a=1,c=2
∵P在双曲线的右支上,
∴|PF1|-|PF2|=2,
∴|PF1|=|PF2|+2,
又双曲线右焦点F2(2,0),
∴|PF1|+|PQ|=|PF2|+4+|PQ|≥|QF2|+2
=$\sqrt{(-2-2)^{2}+{3}^{2}}$+2═5+2=7,(当且仅当Q、P、F2三点共线时取“=”).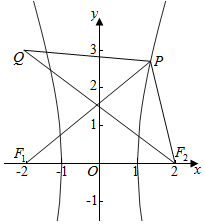
则|PQ|+|PF1|的最小值为7.
故答案为:7.
点评 本题考查双曲线的简单性质,利用双曲线的定义将|PF1|转化为|PF2|+2是关键,考查转化思想与应用不等式的能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的离心率$\sqrt{5}$,则该双曲线的一条渐近线被圆C:x2+y2-2x-3=0截得的弦长为( )
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{8\sqrt{5}}}{5}$ | C. | 3 | D. | 2 |
7.以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
14.抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,O为坐标原点.若|AF|=3,且△AOB的面积为$\frac{{3\sqrt{2}}}{2}$,则点B的纵坐标为( )
| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
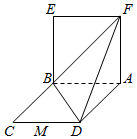 已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.
已知四边形ABCD为平行四边形,BD⊥AD,BD=AD,AB=2,四边形ABEF为正方形,且平面ABEF⊥平面ABCD.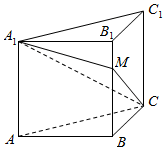 棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
棱长为1的正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.