题目内容
5．
某少数民族的刺绣有着悠久的历史，如图①②③④是刺绣中最简单的四个图案，这些图案都是由小正方形构成的，小正方形的个数越多刺绣越漂亮．现按同样的规律刺绣，设第n个图案包含f（n）个小正方形．（1）求出f（5）的值；
（2）利用合情推理的“归纳推理思想”，归纳出f（n+1）与f（n）之间的关系式，并根据你的关系式求出f（n）的解析式．
分析 （1）先分别观察给出正方体的个数为：1，1+4，1+4+8，…从而得出f（5）；
（2）将（1）总结一般性的规律：f（n+1）与f（n）的关系式，再从总结出来的一般性的规律转化为特殊的数列再求解即得
解答 解：（1）∵f（1）=1，f（2）=5，f（3）=13，f（4）=25，
∴f（2）-f（1）=4=4×1．
f（3）-f（2）=8=4×2，
f（4）-f（3）=12=4×3，
f（5）-f（4）=16=4×4
∴f（5）=25+4×4=41．
（2）由上式规律得出f（n+1）-f（n）=4n．
∴f（2）-f（1）=4×1，
f（3）-f（2）=4×2，
f（4）-f（3）=4×3，
…
f（n-1）-f（n-2）=4•（n-2），
f（n）-f（n-1）=4•（n-1）
∴f（n）-f（1）=4[1+2+…+（n-2）+（n-1）]=2（n-1）•n，
∴f（n）=2n2-2n+1．
点评 本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
15．若复数z=$\frac{3+i}{1+2i}$，则|z|=（ ）
| A． | $\frac{\sqrt{2}}{5}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
16．
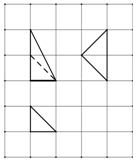某几何体的三视图如图所示，网格纸的小方格是边长为1的正方形，则该几何体中最长的棱长是（ ）
某几何体的三视图如图所示，网格纸的小方格是边长为1的正方形，则该几何体中最长的棱长是（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{6}$ | C． | $\sqrt{7}$ | D． | 3 |
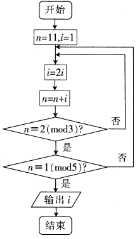《孙子算经》是中国公元四世纪的数学著作，其中接受了求解依次同余式的方法，他是数论中一个重要的定理，又称《中国剩余定理》，如图所示的程序框图的算法就是源于《中国剩余定理》，执行该程序框图，若正整数N除以正整数m后的余数为n，则记为N≡n（modm），例如11≡3（mod4），则输出的等于（ ）
14．如图所给的程序运行结果为S=41，那么判断框中应填入的关于k的条件是（ ）
| A． | k≥6 | B． | k≥5 | C． | k＞6 | D． | k＞5 |