题目内容
6.已知$\overrightarrow a=(sinx,-cosx),\overrightarrow b=(\sqrt{3}cosx,-cosx),f(x)=2\overrightarrow a•\overrightarrow b$(1)求的f(x)解析式;
(2)在△ABC中,a,b,c分别是内角A,B,C的对边,若f(A)=2,b=1,△ABC的面积为$\frac{{\sqrt{3}}}{2}$,求a的值.
分析 (1)利用向量的数量积公式,结合二倍角、辅助角公式,即可求f(x)的解析式;
(2)求出A,c,利用余弦定理求a的值.
解答 解:(1)由题意,f(x)=2$\sqrt{3}$sinxcosx+2cos2x=$\sqrt{3}$sin2x+cos2x+1=2sin(2x+$\frac{π}{6}$)+1…(5分)
(2)∵$f(A)=2sin(2A+\frac{π}{6})+1=2$,∴$sin(2A+\frac{π}{6})=\frac{1}{2}$,
∵A∈(0,π),∴$2A+\frac{π}{6}∈(\frac{π}{6},\frac{13π}{6})$,∴A=$\frac{π}{3}$,
∵△ABC的面积为$\frac{{\sqrt{3}}}{2}$,∴$\frac{1}{2}×1×c×\frac{\sqrt{3}}{2}$=$\frac{{\sqrt{3}}}{2}$,
∴c=2,
∴a=$\sqrt{1+4-2×1×2×\frac{1}{2}}$=$\sqrt{3}$…(12分)
点评 本题考查向量知识的运用,考查三角形面积的计算,考查余弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.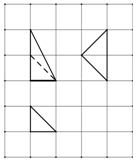 某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
 某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 3 |
14.如图所给的程序运行结果为S=41,那么判断框中应填入的关于k的条件是( )


| A. | k≥6 | B. | k≥5 | C. | k>6 | D. | k>5 |
11.椭圆的对称轴为坐标轴,若长、短轴之和为18,焦距为6,那么椭圆的方程为( )
| A. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
16.命题“?x∈[1,3],x2≤a”为真命题的一个充分不必要条件是( )
| A. | a≤9 | B. | a≥9 | C. | a≤10 | D. | a≥10 |
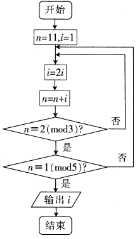 《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( )
《孙子算经》是中国公元四世纪的数学著作,其中接受了求解依次同余式的方法,他是数论中一个重要的定理,又称《中国剩余定理》,如图所示的程序框图的算法就是源于《中国剩余定理》,执行该程序框图,若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如11≡3(mod4),则输出的等于( ) 我国南宋时期的《数学九章》中提出了秦九韶算法来计算多项式的值,在执行下列算法的程序框图时,若输入的n=4,x=2,则输出V的值为( )
我国南宋时期的《数学九章》中提出了秦九韶算法来计算多项式的值,在执行下列算法的程序框图时,若输入的n=4,x=2,则输出V的值为( )