题目内容
16.某班早晨7:30开始上早读课,该班学生小陈和小李在早上7:10至7:30之间到班,且两人在此时间段的任何时刻到班是等可能的.(1)在平面直角坐标系中画出两人到班的所有可能结果表示的区域;
(2)求小陈比小李至少晚5分钟到班的概率.
分析 (Ⅰ)用x,y分别表示小陈、小李到班的时间,则x∈[10,30],y∈[10,30],作出正方形区域得答案;
(Ⅱ)小陈比小李至少晚到5分钟,即x-y≥5,由线性规划知识求出可行域,利用面积比得答案.
解答 解:(Ⅰ)用x,y分别表示小陈、小李到班的时间,
则x∈[10,30],y∈[10,30],
所有可能结果对应坐标平面内一个正方形区域ABCD,
如图所示.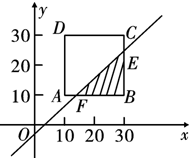
(Ⅱ)小陈比小李至少晚到5分钟,即x-y≥5,
对应区域为△BEF,
所求概率$P=\frac{{{S_{△BEF}}}}{{{S_{ABCD}}}}=\frac{{\frac{1}{2}×15×15}}{20×20}=\frac{9}{32}$.
点评 本题考查几何概型,体现了数学转化思想方法,关键是由题意作出图形,是中档题.

练习册系列答案
相关题目
17.曲线y=-$\frac{1}{x}$在(1,-1)处的切线的斜率为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
11.将一根绳子对折,然后用剪刀在对折过的绳子上任意一处剪断,则得到的三条绳子的长度可以作为三角形的三边形的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
8.在等比数列{an}中,a1=1,a10=3,则a2a3…a8a9等于( )
| A. | 243 | B. | $27\root{5}{27}$ | C. | $\sqrt{3}$ | D. | 81 |
5.已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a9等于( )
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
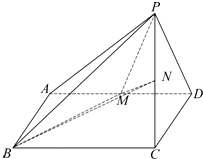 四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.
四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.