题目内容
12.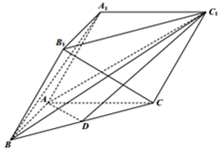 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.(Ⅰ)求证:A1B∥平面ADC1;
(Ⅱ)当BC1=4时,求直线B1C与平面ADC1所成角的正弦值.
分析 (Ⅰ)连接A1C,交AC1于O,连接OD,证明OD∥A1B,即可证明:A1B∥平面ADC1;
(Ⅱ)建立如图所示的坐标系,求出平面ADC1的法向量,利用向量方法,即可求直线B1C与平面ADC1所成角的正弦值.
解答 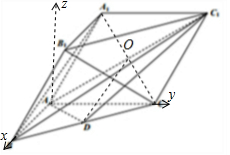 (Ⅰ)证明:连接A1C,交AC1于O,连接OD,
(Ⅰ)证明:连接A1C,交AC1于O,连接OD,
∵D为BC的中点,
∴OD∥A1B,
∵A1B?,OD?平面ADC1,
∴A1B∥平面ADC1;
(Ⅱ)解:建立如图所示的坐标系,则A(0,0,0),D(1,1,0),C1(0,3,$\sqrt{3}$),B1(2,1,$\sqrt{3}$),C(0,2,0),
∴$\overline{AD}$=(1,1,0),$\overrightarrow{A{C}_{1}}$=(0,3,$\sqrt{3}$),
设平面ADC1的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{x+y=0}\\{3y+\sqrt{3}z=0}\end{array}\right.$,$\overrightarrow{n}$=(1,-1,$\sqrt{3}$),
∵$\overrightarrow{{B}_{1}C}$=(-2,1,-$\sqrt{3}$),
∴直线B1C与平面ADC1所成角的正弦值=|$\frac{-2-1-3}{\sqrt{5}•\sqrt{4+1+3}}$|=$\frac{3\sqrt{10}}{10}$.
点评 本题考查线面平行,考查线面角,考查向量方法的运用,属于中档题.

练习册系列答案
相关题目
2.已知双曲线C1:x2-y2=a2(a>0)关于直线y=x-2对称的曲线为C2,若直线2x+3y=6与C2相切,则实数a的值为( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
7.设实数λ>0,若对任意的x∈(0,+∞),不等式eλx-$\frac{lnx}{λ}$≥0恒成立,则λ的最小值为( )
| A. | $\frac{1}{e}$ | B. | $\frac{1}{2e}$ | C. | $\frac{2}{e}$ | D. | $\frac{e}{3}$ |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
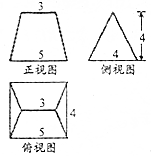

| A. | $\frac{113}{3}$ | B. | 35 | C. | $\frac{104}{3}$ | D. | $\frac{107}{4}$ |
3.《九章算术》是我国古代数学成就的杰出代表,是“算经十书”中最重要的一种,是当时世界上最简练有效的应用数字,它的出现标志中国古代数学形成了完整的体系.其中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢×矢),弧田是由圆弧(简称为弧田弧)和以圆弧的端点为端点的线段(简称为弧田弧)围成的平面图形,公式中“弦”指的是弧田弦的长,“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差.现有一弧田,其弦长AB等于6米,其弧所在圆为圆O,若用上述弧田面积计算公式算得该弧田的面积为$\frac{7}{2}$平方米,则cos∠AOB=( )
| A. | $\frac{1}{25}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{25}$ |
 某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.