题目内容
2.已知双曲线C1:x2-y2=a2(a>0)关于直线y=x-2对称的曲线为C2,若直线2x+3y=6与C2相切,则实数a的值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
分析 求出曲线C2的方程,利用直线2x+3y=6与C2相切,△=0,则实数a的值可求.
解答 解:设C2上的点为(x,y),关于直线y=x-2对称的点的坐标为(y+2,x-2),
代入双曲线C1:x2-y2=a2,可得(y+2)2-(x-2)2=a2,
∵直线2x+3y=6与C2相切,∴联立化简可得5x2+12x-108+9a2=0,△=144-20(-108+9a2)=0,
∵a>0,∴a=$\frac{8\sqrt{5}}{5}$,
故选D.
点评 本题考查曲线的方程,考查直线与曲线位置关系的运用,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
12.已知f(x-3)=2x2-3x+1,则f(1)=( )
| A. | 15 | B. | 21 | C. | 3 | D. | 0 |
13.设集合U={1,2,3,4,5},集合A={x∈Z|x2-5x+4<0},集合B={1,2},则(∁UA)∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,3} | D. | {2,3} |
14.某产品的广告费用x与销售额y的统计数据如表:
用最小二乘法算得的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\widehat{b}$为7,据此预测广告费用为6万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
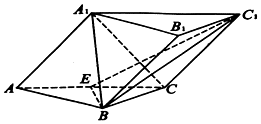 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥平面ABC,AB=BC=2,∠ACB=30°,∠C1CB=120°,BC1⊥A1C,E为AC的中点.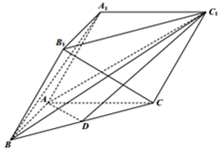 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.