题目内容
3. 某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.(1)求居民月用水量费用y(单位:元)关于月用电量x(单位:吨)的函数解析式;
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占60%,求a,b的值;
(3)若地区居民用水量平均值超过6吨,则说明该地区居民用水没有节约意识在满足(2)的条件下,请你估计A市居民用水是否有节约意识(同一组中的数据用该组区间的中点值作代表).
分析 (1)由题意写出分段函数的解析式即可.
(2)根据题意可得P(y≤16)=P(x≤6)=0.6,即可求出a,b的值.
(3)由用水量的频率分布表和题意,得居民该月用水费用的数据分组与频率分布表,由此能求出该市每户居民该月的平均水费,并判断即可.
解答 解:(1)$y=\left\{{\begin{array}{l}{2x,0≤x≤4}\\{4x-8,4<x≤8}\\{8x-40,x>8}\end{array}}\right.$;
(2)∵y=16时,x=6,
∴P(y≤16)=P(x≤6)=0.6,
∴0.050×2+b×2+0.150×2=0.6,
b×2+a×2+0.025×2=0.4,
∴$\left\{{\begin{array}{l}{a=0.075}\\{b=0.100}\end{array}}\right.$
(3)$\overline x=1•0.050•2+3•0.100•2+5•0.150•2+7•0.100•2+9•0.075•2+11•0.025•2$,
$\overline x=5.5<6$,
∴A市居民用水有节约意识.
点评 本题主要考查平均数频率直方图、考查学生应用意识、运算求解能力、数据处理能力及分析问题解决问题的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.设集合U={1,2,3,4,5},集合A={x∈Z|x2-5x+4<0},集合B={1,2},则(∁UA)∩B=( )
| A. | {1} | B. | {1,2} | C. | {1,3} | D. | {2,3} |
14.某产品的广告费用x与销售额y的统计数据如表:
用最小二乘法算得的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\widehat{b}$为7,据此预测广告费用为6万元时销售额为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 32 | 35 | 45 | 52 |
| A. | 58.5万元 | B. | 77.5万元 | C. | 59万元 | D. | 70万元 |
18.已知x,y满足约束条件$\left\{{\begin{array}{l}{x≤-1}\\{x-y≥-2}\\{x+y+1≥0}\end{array}}\right.$,则目标函数z=3x+y的取值范围为( )
| A. | [-4,-2] | B. | [-4,+∞) | C. | [-3,+∞) | D. | [-3,-2] |
14.在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调查了某地区的100个捐款居民每月平均的经济收入.在捐款超过100元的居民中,每月平均的经济收入没有达到2000元的有60个,达到2000元的有20个;在捐款不超过100元的居民中,每月平均的经济收入没有达到2000元的有10个.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
附:X2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
| 每月平均经济收入达到2000元 | 每月平均经济收入没有达到2000元 | 合计 | |
| 捐款超过 100元 | |||
| 捐款不超 过100元 | |||
| 合计 |
| 参 考 数 据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
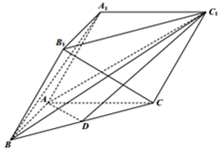 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.