题目内容
2.(x-2)(x+1)5的展开式中,x3的系数是-10(用数字填写答案)分析 求出(x+1)5展开式的含x2与x3项的系数,再计算(x-2)(x+1)5展开式中x3的系数.
解答 解:(x+1)5展开式的通项公式为Tr+1=C5r•x5-r,
令5-r=2,解得r=3,
所以T4=C53•x2=10x2;
令5-r=3,解得r=2,
所以T3=C52•x3=10x3;
所以(x-2)(x+1)5展开式中x3的系数为
10×1+10×(-2)=-10.
故答案为:-10.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
10.一组数据的平均数是4.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A. | 55.2,3.6 | B. | 55.2,56.4 | C. | 64.8,63.6 | D. | 64.8,3.6 |
17.已知函数f(x)=ex+a•e-x+2(a∈R,e为自然对数的底数),若y=f(x)与y=f(f(x))的值域相同,则a的取值范围是( )
| A. | a<0 | B. | a≤-1 | C. | 0<a≤4 | D. | a<0或0<a≤4 |
7.数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),S n为数列{an}前n项和,S100=( )
| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
14.在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调查了某地区的100个捐款居民每月平均的经济收入.在捐款超过100元的居民中,每月平均的经济收入没有达到2000元的有60个,达到2000元的有20个;在捐款不超过100元的居民中,每月平均的经济收入没有达到2000元的有10个.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
附:X2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
| 每月平均经济收入达到2000元 | 每月平均经济收入没有达到2000元 | 合计 | |
| 捐款超过 100元 | |||
| 捐款不超 过100元 | |||
| 合计 |
| 参 考 数 据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
11.偶函数f(x)是定义域为R上的可导函数,当x≥0时,都有f'(x)<2x成立,则不等式f(x-1)+2x>f(x)+1的解集是( )
| A. | $\left\{{\left.x\right|x<\frac{1}{2}}\right\}$ | B. | $\left\{{\left.x\right|x>\frac{1}{2}}\right\}$ | C. | {x|x≠$\frac{1}{2}$} | D. | 实数集R |
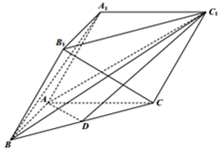 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.