题目内容
17.已知某几何体的三视图如图所示,则该几何体的体积为( )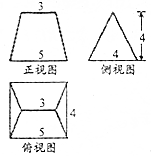
| A. | $\frac{113}{3}$ | B. | 35 | C. | $\frac{104}{3}$ | D. | $\frac{107}{4}$ |
分析 根据三视图可得,该几何体是一个直四棱柱,截取了两个小三棱柱,利用体积公式运算.
解答 解:根据三视图可得,该几何体是一个直四棱柱,截取了两个小三棱柱,
其体积V=${s}_{△ABC}×C{C}_{1}-2×\frac{1}{3}×{s}_{△ABC}×CE$=$\frac{1}{2}×4×4×5-2×\frac{1}{3}×\frac{1}{2}×4×4×1=\frac{104}{3}$.
故选:C
点评 三视图和立体图之间的转换,几何体的体积公式的应用,主要考查学生的空间想象能力和应用能力.属于中档题

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.设实数a∈(0,1),则函数f(x)=x2-(2a+1)x+a2+1有零点的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
10.一组数据的平均数是4.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A. | 55.2,3.6 | B. | 55.2,56.4 | C. | 64.8,63.6 | D. | 64.8,3.6 |
7.数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),S n为数列{an}前n项和,S100=( )
| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )
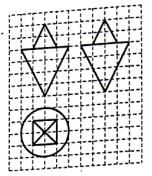

| A. | $\frac{16}{3}(π+1)$ | B. | $\frac{8}{3}(2π+1)$ | C. | 8(2π+1) | D. | 16(π+1) |
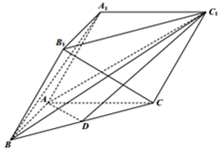 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.