题目内容
3.《九章算术》是我国古代数学成就的杰出代表,是“算经十书”中最重要的一种,是当时世界上最简练有效的应用数字,它的出现标志中国古代数学形成了完整的体系.其中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢×矢),弧田是由圆弧(简称为弧田弧)和以圆弧的端点为端点的线段(简称为弧田弧)围成的平面图形,公式中“弦”指的是弧田弦的长,“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差.现有一弧田,其弦长AB等于6米,其弧所在圆为圆O,若用上述弧田面积计算公式算得该弧田的面积为$\frac{7}{2}$平方米,则cos∠AOB=( )| A. | $\frac{1}{25}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{25}$ |
分析 由弧田面积求出矢=1,设半径为r,圆心到弧田弦的距离为d,列出方程组求出d=4,r=5,从而得到cos∠AOD=$\frac{d}{r}$=$\frac{4}{5}$,再由cos∠AOB=2cos2∠AOD-1,能求出结果.
解答  解:如图,由题意可得:AB=6,
解:如图,由题意可得:AB=6,
弧田面积S=$\frac{1}{2}$(弦×矢+矢2)=$\frac{1}{2}×$(6×矢+矢2)=$\frac{7}{2}$平方米.
解得矢=1,或矢=-7(舍),
设半径为r,圆心到弧田弦的距离为d,
则$\left\{\begin{array}{l}{r-d=1}\\{{r}^{2}=9+{d}^{2}}\end{array}\right.$,解得d=4,r=5,
∴cos∠AOD=$\frac{d}{r}$=$\frac{4}{5}$,
∴cos∠AOB=2cos2∠AOD-1=$\frac{32}{25}$-1=$\frac{7}{25}$.
故选:D.
点评 本题考查角的余弦值的求法,考查同角三角函数关系式、二倍角公式、弧田面积计算公式,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

练习册系列答案
相关题目
14.在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调查了某地区的100个捐款居民每月平均的经济收入.在捐款超过100元的居民中,每月平均的经济收入没有达到2000元的有60个,达到2000元的有20个;在捐款不超过100元的居民中,每月平均的经济收入没有达到2000元的有10个.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
附:X2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)在下图表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否超过100元和居民每月平均的经济收入是否达到2000元有关?
(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量居民中,采用随机抽样方法每次抽取1个居民,共抽取3次,记被抽取的3个居民中经济收入达到2000元的人数为X,求P(X=2)和期望EX的值.
| 每月平均经济收入达到2000元 | 每月平均经济收入没有达到2000元 | 合计 | |
| 捐款超过 100元 | |||
| 捐款不超 过100元 | |||
| 合计 |
| 参 考 数 据 | 当x2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当x2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当x2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当x2>6.635时,有99%的把握判定变量A,B有关联. |
11.偶函数f(x)是定义域为R上的可导函数,当x≥0时,都有f'(x)<2x成立,则不等式f(x-1)+2x>f(x)+1的解集是( )
| A. | $\left\{{\left.x\right|x<\frac{1}{2}}\right\}$ | B. | $\left\{{\left.x\right|x>\frac{1}{2}}\right\}$ | C. | {x|x≠$\frac{1}{2}$} | D. | 实数集R |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的体积为( )
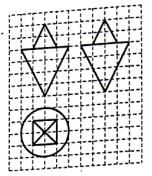

| A. | $\frac{16}{3}(π+1)$ | B. | $\frac{8}{3}(2π+1)$ | C. | 8(2π+1) | D. | 16(π+1) |
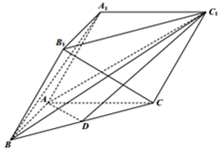 如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.
如图,在三棱柱ABC-A1B1C1中,D为BC的中点,∠BAC=90°,∠A1AC=60°,AB=AC=AA1=2.